题目内容
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=![]() ax2+
ax2+![]() ax+
ax+![]() a(a≠0)交x轴于点A和点B(点A在点B左边),交y轴于点C,连接AC,tan∠CAO=3.
a(a≠0)交x轴于点A和点B(点A在点B左边),交y轴于点C,连接AC,tan∠CAO=3.

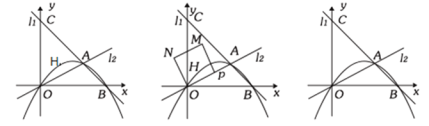
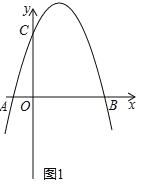
(1)如图1,求抛物线的解析式;
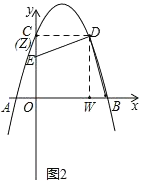
(2)如图2,D是第一象限的抛物线上一点,连接DB,将线段DB绕点D顺时针旋转90°,得到线段DE(点B与点E为对应点),点E恰好落在y轴上,求点D的坐标;
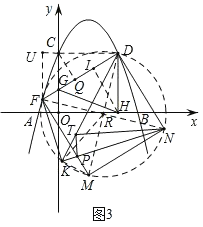
(3)如图3,在(2)的条件下,过点D作x轴的垂线,垂足为H,点F在第二象限的抛物线上,连接DF交y轴于点G,连接GH,sin∠DGH=![]() ,以DF为边作正方形DFMN,P为FM上一点,连接PN,将△MPN沿PN翻折得到△TPN(点M与点T为对应点),连接DT并延长与NP的延长线交于点K,连接FK,若FK=
,以DF为边作正方形DFMN,P为FM上一点,连接PN,将△MPN沿PN翻折得到△TPN(点M与点T为对应点),连接DT并延长与NP的延长线交于点K,连接FK,若FK=![]() ,求cos∠KDN的值.
,求cos∠KDN的值.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)D的坐标为(3,3);(3)
x+3;(2)D的坐标为(3,3);(3)![]()
【解析】
(1)通过抛物线y=![]() 先求出点A的坐标,推出OA的长度,再由tan∠CAO=3求出OC的长度,点C的坐标,代入原解析式即可求出结论;
先求出点A的坐标,推出OA的长度,再由tan∠CAO=3求出OC的长度,点C的坐标,代入原解析式即可求出结论;
(2)如图2,过点D分别作x轴和y轴的垂线,垂足分别为W和Z,证△DZE≌△DWB,得到DZ=DW,由此可知点D的横纵坐标相等,设出点D坐标,代入抛物线解析式即可求出点D坐标;
(3)如图3,连接CD,分别过点C,H作F的垂线,垂足分别为Q,I,过点F作DC的垂线,交DC的延长线于点U,先求出点G坐标,求出直线DG解析式,再求出点F的坐标,即可求出正方形FMND的边长,再求出其对角线FN的长度,最后证点F,K,M,N,D共圆,推出∠KDN=∠KFN,求出∠KFN的余弦值即可.
解:(1)在抛物线y=![]() 中,
中,
当y=0时,x1=﹣1,x2=4,
∴A(﹣1,0),B(4,0),
∴OA=1,
∵tan∠CAO=3,
∴OC=3OA=3,
∴C(0,3),
∴![]() a=3,
a=3,
∴a=2,
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+3;
x+3;
(2)如图2,过点D分别作x轴和y轴的垂线,垂足分别为W和Z,
∵∠ZDW=∠EDB=90°,
∴∠ZDE=∠WDB,
∵∠DZE=∠DWB=90°,DE=DB,
∴△DZE≌△DWB(AAS),
∴DZ=DW,
设点D(k,﹣![]() k2+
k2+![]() k+3),
k+3),
∴k=﹣![]() k2+
k2+![]() k+3,
k+3,
解得,k1=﹣![]() (舍去),k2=3,
(舍去),k2=3,
∴D的坐标为(3,3);
(3)如图3,连接CD,分别过点C,H作F的垂线,垂足分别为Q,I,
∵sin∠DGH=![]()
∴设HI=4m,HG=5m,则IG=3m,
由题意知,四边形OCDH是正方形,
∴CD=DH=3,
∵∠CDQ+∠IDH=90°,∠IDH+∠DHI=90°,
∴∠CDQ=∠DHI,
又∵∠CQD=∠DIH=90°,
∴△CQD≌△DIH(AAS),
设DI=n,
则CQ=DI=n,DQ=HI=4m,
∴IQ=DQ﹣DI=4m﹣n,
∴GQ=GI﹣IQ=3m﹣(4m﹣n)=n﹣m,
∵∠GCQ+∠QCD=90°,∠QCD+∠CDQ=90°,
∴∠GCQ=∠CDQ,
∴△GCQ∽△CDQ,
∴![]()
∴![]()
∴n=2m,
∴CQ=DI=2m,
∴IQ=2m,
∴tan∠CDG=![]() ,
,
∵CD=3,
∴CG=![]() ,
,
∴GO=CO﹣CG=![]() ,
,
设直线DG的解析式为y=kx+![]() ,
,
将点D(3,3)代入,
得,k=![]() ,
,
∴yDG=![]() ,
,
设点F(t,﹣![]() t2+
t2+![]() t+3),
t+3),
则﹣![]() t2+
t2+![]() t+3=
t+3=![]() t+
t+![]() ,解得,t1=3(舍去),t2=﹣
,解得,t1=3(舍去),t2=﹣![]() ,
,
∴F(﹣![]() ,
,![]() )
)
过点F作DC的垂线,交DC的延长线于点U,
则![]() ,
,
∴在Rt△UFD中,
DF=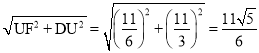 ,
,
由翻折知,△NPM≌△NPT,
∴∠MNP=∠TNP,NM=NT=ND,∠TPN=∠MPN,TP=MP,
又∵NS⊥KD,
∴∠DNS=∠TNS,DS=TS,
∴∠SNK=∠TNP+∠TNS=![]() ×90°=45°,
×90°=45°,
∴∠SKN=45°,
∵∠TPK=180°﹣∠TPN,∠MPK=180°﹣∠MPN,
∴∠TPK=∠MPK,
又∵PK=PK,
∴△TPK≌△MPK(SAS),
∴∠MKP=∠TKP=45°,
∴∠DKM=∠MKP+∠TKP=90°,
连接FN,DM,交点为R,再连接RK,
则RK=RF=RD=RN=RM,
则点F,D,N,M,K同在⊙R上,FN为直径,
∴∠FKN=90°,∠KDN=∠KFN,
∵FN=![]() ,
,
∴在Rt△FKN中,
∴cos∠KDN=cos∠KFN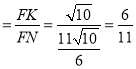 .
.

【题目】某农科所在相同条件下做某作物种子发芽率的实验,结果如下表所示:
种子个数 | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
发芽种子个数 | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
发芽种子率 | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
下面有四个推断:
①种子个数是700时,发芽种子的个数是624,所以种子发芽的概率是0.891;
②随着参加实验的种子数量的增加,发芽种子的频率在0.9附近摆动,显示出一定的稳定性,可以估计种子发芽的概率约为0.9(精确到0.1);
③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率;
④若用频率估计种子发芽的概率约为0.9,则可以估计![]() 种子中大约有
种子中大约有![]() 的种子不能发芽.
的种子不能发芽.
其中合理的是______.