题目内容
【题目】阅读下列材料,并按要求解答.
(模型介绍)
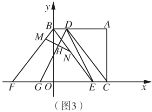
如图①,C是线段A、B上一点E、F在AB同侧,且∠A=∠B=∠ECF=90°,看上去像一个“K“,我们称图①为“K”型图.
(性质探究)
性质1:如图①,若EC=FC,△ACE≌△BFC
性质2:如图①,若EC≠FC,△ACE~△BFC且相似比不为1.
(模型应用)
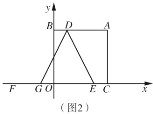
应用1:如图②,在四边形ABCD中,∠ADC=90°,AD=1,CD=2,BC=2![]() ,AB=5.求BD.
,AB=5.求BD.
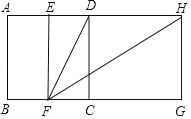
应用2:如图③,已知△ABC,分别以AB、AC为边向外作正方形ABGF、正方形ACDE,AH⊥BC,连接EF.交AH的反向延长线于点K,证明:K为EF中点.
(1)请你完成性质1的证明过程;
(2)请分别解答应用1,应用2提出的问题.
【答案】(1)证明见解析;(2)应用1: BD=4![]() ;应用2:证明见解析.
;应用2:证明见解析.
【解析】
(1)根据AAS即可证明;
(2)①应用1:如图2中,连接AC,作BH⊥DC交DC的延长线与H.首先证明符合“k模型”,利用性质2根据相似三角形的性质即可解决问题;
②应用2:如图③中,作FM⊥KH于M,EN⊥HN于N.由性质1可知:△ABH≌△FAM,△AHC≌△ENA,推出FM=AH,AH=EN,推出FM=EN,再证明△FKN≌△EKN即可解决问题.
(1)如图①中,
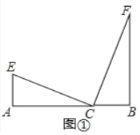
∵∠A=∠ECF=∠B=90°,
∴∠ACE+∠BCF=90°,∠BCF+∠F=90°,
∴∠ACE=∠F,∵EC=CF,
∴△ACE≌△BFC.
(2)①应用1:如图2中,连接AC,作BH⊥DC交DC的延长线与H.
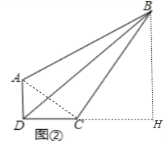
在Rt△ADC中,∵∠ADC=90°,AD=1,CD=2,
∴AC=![]() =
=![]() ,
,
∵AC2+BC2=5+20=25,AB2=52=25,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴∠ADC=∠ACB=∠CHB=90°,
∴符合“K”型图,
∴△ACD∽△CBH,
∴![]() ,
,
∴![]() ,
,
∵CH=2,BH=4,
∴DH=4,
在Rt△BDH中,BD=![]() =4
=4![]() .
.
应用2:如图③中,作FM⊥KH于M,EN⊥HN于N,
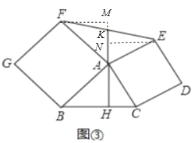
由性质1可知:△ABH≌△FAM,△AHC≌△ENA,
∴FM=AH,AH=EN,
∴FM=EN,
∵∠FKM=∠EKN,∠M=∠ENK=90°,
∴△FKN≌△EKN,
∴FK=KE,
∴K为EF中点.

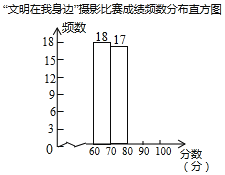
【题目】某校举行了“文明在我身边”摄影比赛,已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分步赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
“文明在我身边”摄影比赛成绩统计表
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x≤100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= .
(2)补全数分布直方图;
(3)若80分以上的作品将被组织展评,试估计全校被展评作品数量是多少?