��Ŀ����
����Ŀ����֪����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬ֱ��
Ϊ����ԭ�㣬ֱ��![]() �ֱ�
�ֱ�![]() �ᣬ
�ᣬ![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() �ڵ�һ���ޣ�����
�ڵ�һ���ޣ�����![]() ��
��![]() ���ı���
���ı���![]() �������Σ�
��������

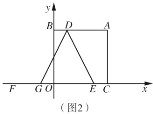
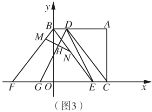
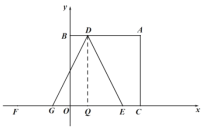
��1����ͼ1����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����ͼ2����![]() �ֱ���
�ֱ���![]() �ϣ���
�ϣ���![]() ����
����![]() ��ĶԳƵ�Ϊ��
��ĶԳƵ�Ϊ��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() ��
��![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ����ֱ��д���Ա���
֮��ĺ�����ϵʽ����ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����ͼ3���ڣ�2���������£�����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��![]() �ϣ�����
�ϣ�����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ����2��
����2��![]() ����3��32
����3��32
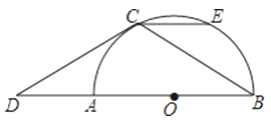
��������
��1������C�����꣬�ٴ������ʽ�����k��
��2�����ݵ�E����y��ĶԳƵ�Ϊ��F��EG=2FG���Եó�OG��OE�Ĺ�ϵ���Ӷ��ó�GE��t�Ĺ�ϵ���ٸ��������������ʽ�������S��
��3����![]() ����
����![]() ��
��![]() ����
����![]() �У����ݹ��ɶ������n���ӳ�
�У����ݹ��ɶ������n���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ����
����![]() ���Ӷ�֤��
���Ӷ�֤��![]() ����
����![]() �У����ݹ��ɶ������m���Ӷ����S.
�У����ݹ��ɶ������m���Ӷ����S.
�⣺��1����![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��![]() ��
��
���ı���![]() �������Σ�
��������
��![]() ��
��
��![]() ��
��
�������ʽ��![]() ��
��
���![]() ��
��
��![]() ��
��
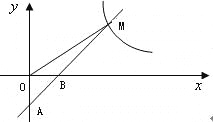
��2����ͼ������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��![]() ��
��
���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��![]() ��
��
�ߵ�![]() ���
���![]() ����
����![]() ��Գƣ�
��Գƣ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
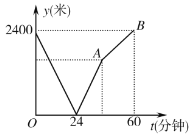
��3����ͼ����![]() ����
����![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
���![]() ��
��![]() ���ᣩ��
���ᣩ��
��![]() ��
��
�ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() �Ľ���Ϊ��
�Ľ���Ϊ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�֡�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
���![]() ���ᣩ��
���ᣩ��
��![]() ��
��
��![]() ��
��
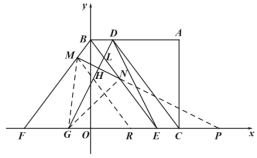

 ��������������������ϵ�д�
��������������������ϵ�д�