题目内容
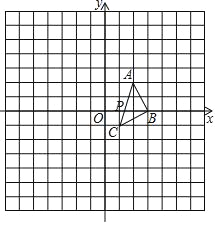
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(3,0),C(1,﹣1),AC交x轴于点P.
(1)∠ACB的度数为_____;
(2)P点坐标为______;
(3)以点O为位似中心,将△ABC放大为原来的2倍,请在图中画出所有符合条件的三角形.
【答案】(1)45°;(2)(![]() ,0);(3)见解析.
,0);(3)见解析.
【解析】
(1)由题意得到三角形ABC为等腰直角三角形,即可确定出所求角度数;
(2)利用待定系数法求出直线AC解析式,即可确定出P坐标;
(3)以为位似中心,将△ABC放大为原来的2倍,画出相应图形,如图所示.
(1)∵∠ABC=90°,AB=CB=![]() ,
,
∴△ABC为等腰直角三角形,
∴∠ACB=45°;
故答案为:45°;
(2)由题意得:A(2,2),C(1,﹣1),
设直线AC解析式为y=kx+b,
把A与C坐标代入得:![]() ,
,
解得:![]() ,即直线AC解析式为y=3x﹣4,
,即直线AC解析式为y=3x﹣4,
令y=0,得到x=![]() ,
,
则P的坐标为(![]() ,0);
,0);
故答案为:(![]() ,0);
,0);
(3)如图所示:△A1B1C1和△A2B2C2为所求三角形.

练习册系列答案
相关题目