��Ŀ����
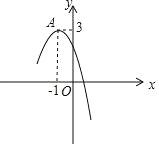
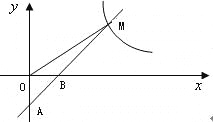
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,��P��ԭ��O����,��x��������ÿ��1����λ�����ٶ��˶�t(t>0)��,������![]() ������O�͵�P.��֪����ABCD����������ΪA(1,0),B(1,4),D(4,0).
������O�͵�P.��֪����ABCD����������ΪA(1,0),B(1,4),D(4,0).
��1����c,b(���ú�t�Ĵ���ʽ��ʾ)��
��2����t>1ʱ�����������߶�![]() ���ڵ�M����x���ڵ�E.�ڵ�P���˶������У�����Ϊ��AMP�Ĵ�С�Ƿ��仯?���仯��˵�����ɣ������䣬�����AMP��ֵ��
���ڵ�M����x���ڵ�E.�ڵ�P���˶������У�����Ϊ��AMP�Ĵ�С�Ƿ��仯?���仯��˵�����ɣ������䣬�����AMP��ֵ��
��3����PΪx�������ϵĶ��㣬�߶�PM���߶�BC�й�����ʱ�����P�ĺ�����t��ȡֵ��Χ.

���𰸡�(1) b=t��(2) ��������EMP=45�㣻��3�����߶�PM���߶�BC�й�����ʱ����P�ĺ�����t ��ȡֵ��ΧΪ5�Qt�Q8.
��������
��1����������y=x2+bx+c������O�͵�P������O��P��������뷽�̼������c��b��
��2����x=-1ʱ��y=-1-t�����M�����꣬�����á�AMP�Ķ�����
��3����ֱ��PM�Ľ���ʽΪ![]() ��P(t��0������M��-1��-1-t��������⣬�ٸ����߶�PM���߶�BC�й����������Χ��
��P(t��0������M��-1��-1-t��������⣬�ٸ����߶�PM���߶�BC�й����������Χ��
(1)��x=0,y=0����![]() ����c=0��
����c=0��
�ٰ�x=t,y=0����![]() ,��
,��![]() ��
��
��t>0��
��b=t��
(2)���䡣
�������ߵĽ���ʽΪ��![]() ����M�ĺ�����Ϊ1��
����M�ĺ�����Ϊ1��
�൱x=-1ʱ��y=-1t��
��M(-1,-1t)��
��EM=t+1��EP=t+1
��EM=EP��
�ߡ�PEM=90����
���EMP=45����
��3����ֱ��PM�Ľ���ʽΪ![]() ��m��0��
��m��0��
��ֱ��PM������P(t��0������M��-1��-1-t��
![]()
![]()
M=1��n=-t
��ֱ��PM�Ľ���ʽΪ![]()
��PM����B��1��-4��ʱ����1-t=-4�����t=5
��PM����C,(4,-4)ʱ����4-t=-4�����t=8
�൱�߶�PM���߶�BC�й�����ʱ����P�ĺ�����t ��ȡֵ��ΧΪ5�Qt�Q8.