题目内容
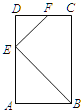
【题目】宽与长的比是![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC的平分线,交AD的延长线于点H,作HG⊥BC,交BC的延长线于点G,则下列矩形是黄金矩形的是( )
(约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC的平分线,交AD的延长线于点H,作HG⊥BC,交BC的延长线于点G,则下列矩形是黄金矩形的是( )
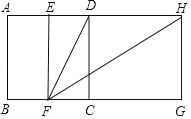
A.矩形ABFEB.矩形EFCDC.矩形EFGHD.矩形DCGH
【答案】C
【解析】
设正方形ABCD的边长为2,根据勾股定理求出DF,根据黄金矩形的概念判断即可.
解:设正方形ABCD的边长为2,
∵点E,F分别为AD,BC的中点,
∴![]() =
=![]() ,DF=
,DF=![]() =
=![]() ,
,
∴矩形ABFE不是黄金矩形,A错误;
同理,矩形EFCD不是黄金矩形,B错误;
∵FH是∠DFC的平分线,
∴∠DFH=∠GFH,
∵AH∥BG,
∴∠DFH=∠GFH,
∴∠DHF=∠GFH,
∴∠DFH=∠DHF,
∴DH=DF=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴矩形EFGH是黄金矩形,C正确;
![]() =
=![]() =
=![]() ,
,
∴矩形DCGH不是黄金矩形,D错误;
故选:C.

练习册系列答案
相关题目