题目内容
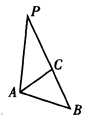
如图, DE是
的中位线，M是DE的中点, CM的延长线交AB于N，那么
=_________________.
的中位线，M是DE的中点, CM的延长线交AB于N，那么=_________________.1：5
解析：根据三角形的中位线定理，把各边的关系转化为面积的关系来解答．
解答：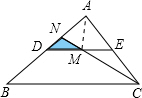
解：DE是中位线，所以S△ADE=
S△ABC，
S四边形DBCE=
S△ABC，连接AM，AE=CE，所以S△AEM=S△MEC
所以S△MEC=
×S△ABC=
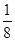S△ABC，所以S四边形DBCM=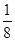（-）S△ABC=
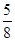S△ABC，
∵DM：BC=1：4，所以S△NDM：S四边形DBCM=1：15．所以S△NDM=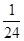
S△ABC
S△AMN=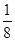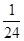（-）S△ABC=
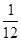S△ABCS四边形ANME=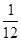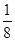（+）S△ABC=
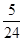S△ABC
所以S△NDM：S四边形ANME=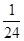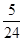：=1：5．
点评：解答此题，首先根据相似三角形的面积比等于相似比的平方，求出S△ADE=S△ABC，便可找到突破口解答．
解答：
解：DE是中位线，所以S△ADE=S△ABC，S四边形DBCE=
S△ABC，连接AM，AE=CE，所以S△AEM=S△MEC所以S△MEC=
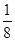×S△ABC=S△ABC，所以S四边形DBCM=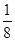（-）S△ABC=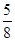S△ABC，∵DM：BC=1：4，所以S△NDM：S四边形DBCM=1：15．所以S△NDM=
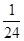S△ABCS△AMN=（
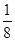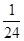-）S△ABC=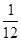S△ABCS四边形ANME=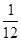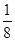（+）S△ABC=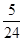S△ABC所以S△NDM：S四边形ANME=
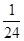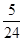：=1：5．点评：解答此题，首先根据相似三角形的面积比等于相似比的平方，求出S△ADE=
S△ABC，便可找到突破口解答．
练习册系列答案
相关题目
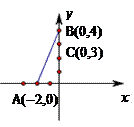
0，4）、B（2，4），它的最高点纵坐标为
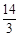，点P是第一象限抛物线上一点且PA=PO，过点P的直线分别交射线AB、x正半轴于C、D．设AC=m，OD=n．
=
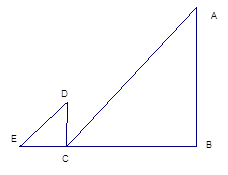
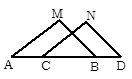
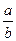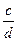，判断代数式
-
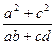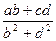+1值的符号
=
=
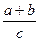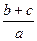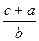，求
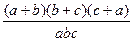的值。