题目内容
如图,在△ABC中,AB=8,BC=7,AC=6,延长边BC到点P,使得△PAB与△PCA相似.则PC的长是( ).
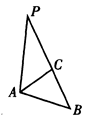

| A.7 | B.8 | C.9 | D.10 |
C
设PA=x,PC=y,
∵△PAB∽△PCA,
∴PA:AB=PC:CA,PB:AB=PA:CA,
∴x:8=y:6①,
(y+7):8=x:6②,
解关于①②的方程组得
x=12,y=9,
故PC=9.
故答案是C.
考查了相似三角形的性质、解方程的知识
∵△PAB∽△PCA,
∴PA:AB=PC:CA,PB:AB=PA:CA,
∴x:8=y:6①,
(y+7):8=x:6②,
解关于①②的方程组得
x=12,y=9,
故PC=9.
故答案是C.
考查了相似三角形的性质、解方程的知识

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
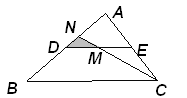
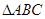 的中位线,M是DE的中点, CM的延长线交AB于N,那么
的中位线,M是DE的中点, CM的延长线交AB于N,那么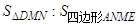 =_________________.
=_________________.
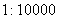 的地图上,某建筑物在图上的面积为50 cm2,则该建筑物实际占地面积为
的地图上,某建筑物在图上的面积为50 cm2,则该建筑物实际占地面积为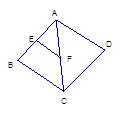
 的AB,AC边上的点,
的AB,AC边上的点,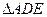 .
.
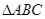 中,若
中,若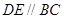 ,
,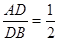 ,
,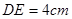 ,求BC的长.
,求BC的长.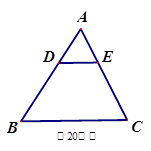
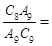 .
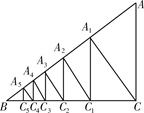
.
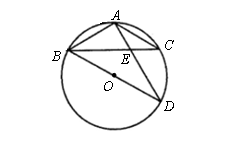
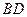 为⊙O的直径,
为⊙O的直径, ,
,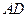 交
交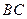 于
于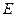 ,
,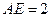 ,
,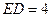 .
.
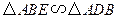 .
. (2)若AD=9cm,DE=6cm,求BE及EF的长.
(2)若AD=9cm,DE=6cm,求BE及EF的长.