题目内容
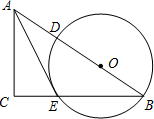
⊙O是△ABC的外接圆,AB是直径,过点C的切线与AB的延长线相交于点D,AE⊥DC交DC于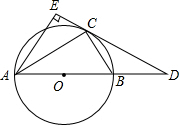 点E.
点E.
(1)求证:AC是∠EAB的平分线;
(2)若圆的半径为3,BD=2,DC=4,求AE和BC.
 点E.
点E.(1)求证:AC是∠EAB的平分线;
(2)若圆的半径为3,BD=2,DC=4,求AE和BC.
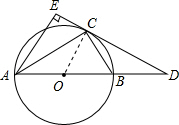
(1)证明:连接OC,
∵ED为圆O的切线,
∴OC⊥ED,
又AE⊥ED,
∴OC∥EA,
∴∠EAC=∠ACO,
又OA=OC,∴∠OAC=∠ACO,
∴∠EAC=∠OAC,即AC是∠EAB的平分线;
(2)∵OC∥AE,
∴∠OCD=∠E,∠COD=∠EAD,
∴△OCD∽△DEA,
∴
=
,即
=
,
解得:AE=
,
∵CD=4,BD=2,AD=8,
即CD2=BD•AD,且夹角∠D为公共角,
∴△BCD∽△ACD,且相似比=
=
,
∴
=
,即AC=2BC,
∵AB为圆O的直径,∴∠ACB=90°,
在Rt△ABC中,根据勾股定理得:AC2+BC2=AB2,
即4BC2+BC2=36,解得:BC=
.
∵ED为圆O的切线,
∴OC⊥ED,
又AE⊥ED,
∴OC∥EA,
∴∠EAC=∠ACO,
又OA=OC,∴∠OAC=∠ACO,
∴∠EAC=∠OAC,即AC是∠EAB的平分线;
(2)∵OC∥AE,
∴∠OCD=∠E,∠COD=∠EAD,
∴△OCD∽△DEA,
∴
| OC |
| AE |
| OD |
| AD |
| 3 |
| AE |
| 5 |
| 8 |
解得:AE=
| 24 |
| 5 |
∵CD=4,BD=2,AD=8,
即CD2=BD•AD,且夹角∠D为公共角,
∴△BCD∽△ACD,且相似比=
| 4 |
| 8 |
| 1 |
| 2 |
∴
| BC |
| AC |
| 1 |
| 2 |
∵AB为圆O的直径,∴∠ACB=90°,
在Rt△ABC中,根据勾股定理得:AC2+BC2=AB2,
即4BC2+BC2=36,解得:BC=
6
| ||
| 5 |


练习册系列答案
相关题目
 ,垂足为F.
,垂足为F.