题目内容
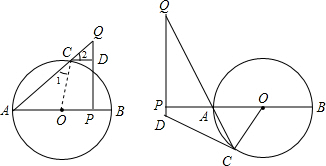
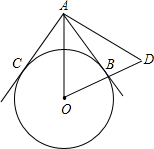
如图,P是⊙O外一点,PA是⊙O的切线,PO=26cm,PA=24cm,则⊙O的周长为( )

| A.18πcm | B.16πcm | C.20πcm | D.24πcm |

如图,连接OA.

∵PA是⊙O的切线,
∴OA⊥AP,即∠OAP=90°.
又∵PO=26cm,PA=24cm,
∴根据勾股定理,得
OA=
=
=10cm,
∴⊙O的周长为:2π•OA=2π×10=20π(cm).
故选C.

∵PA是⊙O的切线,
∴OA⊥AP,即∠OAP=90°.
又∵PO=26cm,PA=24cm,
∴根据勾股定理,得
OA=
| PO2-PA2 |
| 262-242 |
∴⊙O的周长为:2π•OA=2π×10=20π(cm).
故选C.

练习册系列答案
相关题目


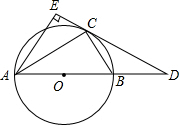 点E.
点E.