题目内容
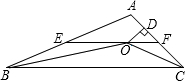
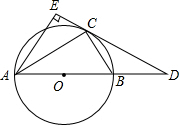
如图,∠C=90°,∠CAE=∠ABC,AC=2,BC=3.
(1)判断AE与⊙O的位置关系,并说明理由;
(2)求OB的长.
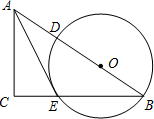
(1)判断AE与⊙O的位置关系,并说明理由;
(2)求OB的长.

(1)证明:连接OE,
∵OE=OB,
∴∠OEB=∠OBE,
又∵∠CAE=∠ABC,
∴∠OEB=∠ABC=∠CAE,
∴∠AEC+∠OEB=90°,
∴∠AEO=90°,
∴AE与⊙O相切.
(2)过点O作OM⊥BE,于点M,
∵∠C=∠C=90°,∠CAE=∠ABC,
∴△ACE∽△BCA,
∴
=
,
∴CE=
×2=
,BE=
,
则BM=
,
AB=
=
,
∵∠C=90°,∠OMB=90°,
∴OM∥AC,
∴△BOM∽△BAC,
∴
=
,
∴
=
=
,
∴OB=
.

∵OE=OB,
∴∠OEB=∠OBE,
又∵∠CAE=∠ABC,
∴∠OEB=∠ABC=∠CAE,
∴∠AEC+∠OEB=90°,
∴∠AEO=90°,
∴AE与⊙O相切.
(2)过点O作OM⊥BE,于点M,
∵∠C=∠C=90°,∠CAE=∠ABC,
∴△ACE∽△BCA,
∴
| CE |
| AC |
| AC |
| BC |
∴CE=
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
则BM=
| 5 |
| 6 |
AB=
| 22+32 |
| 13 |
∵∠C=90°,∠OMB=90°,
∴OM∥AC,
∴△BOM∽△BAC,
∴
| BO |
| AB |
| BM |
| BC |
∴
| OB | ||
|
| ||
| 3 |
| 5 |
| 18 |
∴OB=
5
| ||
| 18 |


练习册系列答案
相关题目

 点E.
点E.