题目内容
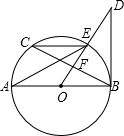
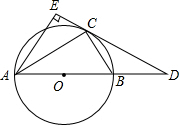
如图,在△ABC中,AB=AC,以AB为直径的圆O交BC于点D,交AC于点E,过点D作DF⊥AC ,垂足为F.
,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若过A点且与BC平行的直线交BE的延长线于G点,连接CG.当△ABC是等边三角形时,求∠AGC的度数.
 ,垂足为F.
,垂足为F.(1)求证:DF为⊙O的切线;
(2)若过A点且与BC平行的直线交BE的延长线于G点,连接CG.当△ABC是等边三角形时,求∠AGC的度数.
(1)证明:连接AD,OD,
∵AB是⊙O的直径,
∴AD⊥BC.(2分)
∵△ABC是等腰三角形,
∴BD=DC,
又∵AO=BO,
∴OD是△ABC的中位线,
∴OD∥AC.
∵DF⊥AC,(4分)
∴DF⊥OD,
∴DF是⊙O的切线.(5分)
(2)∵AB是⊙O的直径,
∴BG⊥AC.
∵△ABC是等边三角形,
∴BG是AC的垂直平分线,
∴GA=GC.(7分)
又∵AG∥BC,∠ACB=60°,
∴∠CAG=∠ACB=60°.
∴△ACG是等边三角形.
∴∠AGC=60°.(9分)

∵AB是⊙O的直径,
∴AD⊥BC.(2分)
∵△ABC是等腰三角形,
∴BD=DC,
又∵AO=BO,
∴OD是△ABC的中位线,
∴OD∥AC.
∵DF⊥AC,(4分)
∴DF⊥OD,
∴DF是⊙O的切线.(5分)
(2)∵AB是⊙O的直径,
∴BG⊥AC.
∵△ABC是等边三角形,
∴BG是AC的垂直平分线,
∴GA=GC.(7分)
又∵AG∥BC,∠ACB=60°,
∴∠CAG=∠ACB=60°.
∴△ACG是等边三角形.
∴∠AGC=60°.(9分)


练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目








 点E.
点E.