题目内容
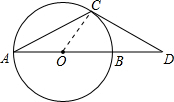
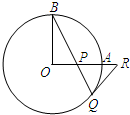
如图，AB是⊙O的直径，弦AC与AB成30°角，CD与⊙O切于C，交AB的延长线于D，
求证：BD=OB．
求证：BD=OB．
证明：连接OC，
∵CD与圆0相切，
∴OC⊥CD，
∴∠OCD=90°，
∵OA=OC，
∴∠A=∠OCA=30°，
∵∠COD为△AOC的外角，
∴∠COD=60°，
∴∠D=30°，
∴OC=
OD，
∴OB=
OD，即B为OD的中点，
则OB=BD．
∵CD与圆0相切，
∴OC⊥CD，
∴∠OCD=90°，
∵OA=OC，
∴∠A=∠OCA=30°，
∵∠COD为△AOC的外角，
∴∠COD=60°，
∴∠D=30°，
∴OC=
| 1 |
| 2 |
∴OB=
| 1 |
| 2 |
则OB=BD．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
点E．