题目内容
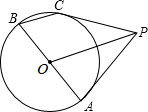
菱形的对角线交点为O,以O为圆心,O到菱形一边的距离为半径的圆与另三边的位置关系是______.
证明:菱形对角线互相垂直平分,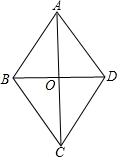
所以AO=CO,BO=DO,AB=BC=CD=DA,
∴△ABO≌△BCO≌△CDO≌△DAO,
∴△ABO、△BCO、△CDO、△DAO的面积相等,
又∵AB=BC=CD=DA,
∴△ABO、△BCO、△CDO、△DAO斜边上的高相等,
即O到AB、BC、CD、DA的距离相等,
∴O到菱形一边的距离为半径的圆与另三边的位置关系是相切,
故答案为:相切.

所以AO=CO,BO=DO,AB=BC=CD=DA,
∴△ABO≌△BCO≌△CDO≌△DAO,
∴△ABO、△BCO、△CDO、△DAO的面积相等,
又∵AB=BC=CD=DA,
∴△ABO、△BCO、△CDO、△DAO斜边上的高相等,
即O到AB、BC、CD、DA的距离相等,
∴O到菱形一边的距离为半径的圆与另三边的位置关系是相切,
故答案为:相切.

练习册系列答案
相关题目

 点E.
点E.