题目内容
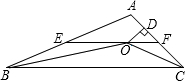
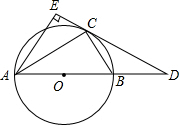
如图,矩形ABCD,AD=8,DC=6,在对角线AC上取一点O,以OC为半径的圆切AD于E,交BC于F,交CD于G.
(1)求⊙O的半径R;
(2)设∠BFE=α,∠CED=β,请写出α,β,90°三者之间的关系式(只需写出一个)并证明你的结论.

(1)求⊙O的半径R;
(2)设∠BFE=α,∠CED=β,请写出α,β,90°三者之间的关系式(只需写出一个)并证明你的结论.

(1)连接OE,则OE⊥AD,
∴△AOE∽△ACD
∴
=
∵矩形ABCD
∴AC=
=
=10
∴
=
解得R=
∴⊙O的半径R=
;
(2)如图,连接CE,
∵AD是圆的切线,
∴β=∠CFE,
∵∠BFE+∠CFE=180°
∴α+β=2×90°=180°.

∴△AOE∽△ACD
∴
| AO |
| AC |
| OE |
| CD |
∵矩形ABCD
∴AC=
| AD2+DC2 |
| 82+62 |
∴
| 10-R |
| 10 |
| R |
| 6 |
解得R=
| 15 |
| 4 |
∴⊙O的半径R=
| 15 |
| 4 |
(2)如图,连接CE,
∵AD是圆的切线,
∴β=∠CFE,
∵∠BFE+∠CFE=180°
∴α+β=2×90°=180°.


练习册系列答案
相关题目




 点E.
点E.