题目内容
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A(2,4),B(n,﹣2)两点.
(m≠0)的图象相交于A(2,4),B(n,﹣2)两点.
(1)求一次函数和反比例函数的表达式;
(2)点C是第一象限内反比例函数图象上的一点,且点C在A的右侧,过点C作CD平行于y轴交直线AB于点D,若以C为圆心,CD长为半径的⊙C恰好与y轴相切,求点C的坐标.
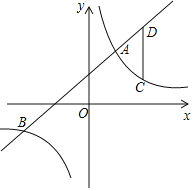
【答案】(1)y=![]() ,y=x+2;(2)点C(4,2)
,y=x+2;(2)点C(4,2)
【解析】
(1)利用待定系数法可求解析式;
(2)设点C(a,![]() ),则点D(a,a+2),可求CD的长,由以C为圆心,CD长为半径的⊙C恰好与y轴相切,可得a=a+2﹣
),则点D(a,a+2),可求CD的长,由以C为圆心,CD长为半径的⊙C恰好与y轴相切,可得a=a+2﹣![]() ,即可求解.
,即可求解.
解:(1)∵A(2,4),B(n,﹣2)在反比例函数y=![]() (m≠0)的图象上,
(m≠0)的图象上,
∴m=2×4=8,﹣2=![]() ,
,
∴n=﹣4,
∴反比例函数的解析式为:y=![]() ;
;
∵一次函数y=kx+b过A(2,4),B(n,﹣2),
∴![]()
∴![]() ,
,
∴一次函数解析式为:y=x+2;
(2)设点C(a,![]() ),则点D(a,a+2),
),则点D(a,a+2),
∴CD=a+2﹣![]() ,
,
∵以C为圆心,CD长为半径的⊙C恰好与y轴相切,
∴a=a+2﹣![]()
∴a=4,
∴点C(4,2).

 名校课堂系列答案
名校课堂系列答案【题目】某校七年级有学生400人,为了解这个年级普及安全教育的情况,随机抽取了20名学生,进行安全教育考试,测试成绩(百分制)如下:
71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
(1)请补全七年级20名学生安全教育测试成绩频数分布直方图;
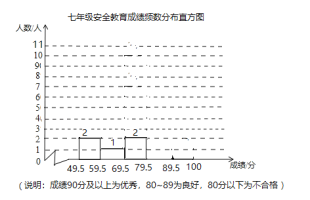
(2)样本数据的平均数、中位数、众数、优秀率如下表所示,请补充完整;
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 85.4 |
|
|
|
(3)估计七年级成绩优秀的学生人数约为_________人.
(4)学校有安全教育老师男女各2名,现从这4名老师中随机挑选2名参加“安全教育”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.