Question

【题目】某校七年级有学生400人，为了解这个年级普及安全教育的情况，随机抽取了20名学生，进行安全教育考试，测试成绩（百分制）如下：

71 94 87 92 55 94 98 78 86 94

62 99 94 51 88 97 94 98 85 91

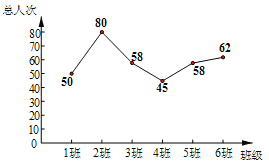
（1）请补全七年级20名学生安全教育测试成绩频数分布直方图；

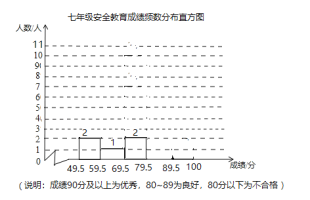
（2）样本数据的平均数、中位数、众数、优秀率如下表所示，请补充完整；

年级	平均数	中位数	众数	优秀率
七年级	85.4

（3）估计七年级成绩优秀的学生人数约为_________人．

（4）学校有安全教育老师男女各2名，现从这4名老师中随机挑选2名参加“安全教育”宣传活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．

Answer 1

【答案】（1）补全图见解析 ；（2）91.5，94 ；（3）220 ；（4）

【解析】

（1）由收集的数据即可得；根据题意不全频数分布直方图即可；

（2）根据众数和中位数的定义求解可得；

（3）根据题意列式计算即可；

（4）列表得出所有等可能的情况数，找出刚好抽到一男一女的情况数，即可求出所求的概率．

（1）由收集的数据可得：79.589.5有4人，89.5100有11人，

补全七年级20名学生安全教育频数分布直方图如图所示：

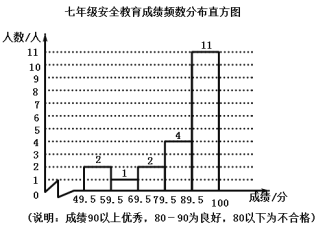
（2）七年级20名学生安全教育考试成绩按从小到大的顺序排列为：

51 55 62 71788586878891 92949494 94 9497 9898 99
∴中位数为分；
∵94分出现的次数最多，故众数为94分；

故答案为：91.5，94；

（3）400×55%=220（人），
答：七年级成绩优秀的学生人数约为220人；

（4）列表如下：

	男	男	女	女
男		（男，男）	（女，男）	（女，男）
男	（男，男）		（女，男）	（女，男）
女	（男，女）	（男，女）		（女，女）
女	（男，女）	（男，女）	（女，女）

得到所有等可能的情况有12种，其中恰好抽中一男一女的情况有8种，
所以恰好选到1名男生和1名女生的概率．