题目内容
【题目】在平面直角坐标系![]() 中,点A的坐标为
中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,抛物线
,抛物线![]() 的顶点为C.
的顶点为C.
(1)若抛物线经过点B时,求顶点C的坐标;
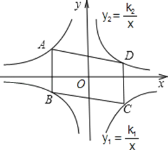
(2)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求a的取值范围;
恰有一个公共点,结合函数图象,求a的取值范围;
(3)若满足不等式![]() 的x的最大值为3,直接写出实数a的值.
的x的最大值为3,直接写出实数a的值.
【答案】(1)![]() ;(2)a的取值范围是
;(2)a的取值范围是![]() 或a=
或a=![]() ;(3)
;(3)![]() .
.
【解析】
(1)将B点坐标代入抛物线即可求出![]() 的值,从而求出抛物线的解析式,再根据顶点坐标公式即可求出顶点坐标;
的值,从而求出抛物线的解析式,再根据顶点坐标公式即可求出顶点坐标;
(2)讲A点和B点的坐标分别代入抛物线解析式即可求出相应的![]() 值,通过观察图象,上下移动图象即可知道抛物线与线段AB有交点时
值,通过观察图象,上下移动图象即可知道抛物线与线段AB有交点时![]() 的范围;
的范围;
(3)抛物线![]() 的对称轴为
的对称轴为![]() ,抛物线开口向上,当
,抛物线开口向上,当![]() 时,
时,![]() 越来越大,则
越来越大,则![]() 的x的最大值为3,可知,当
的x的最大值为3,可知,当![]() 时,
时,![]() ,代入即可求出
,代入即可求出![]() 的值.
的值.
解:(1)依据题意,将得点B的坐标![]() 代入抛物线得:
代入抛物线得:
![]() ,
,
解得![]() .
.
此时,![]() .
.
所以顶点C的坐标为![]() .
.
(2)当抛物线过![]() 时,
时,![]() ,此时,
,此时,![]() .
.
当抛物线过![]() 时,
时,![]() ,此时,
,此时,![]() .
.
当抛物线顶点在线段AB上时,a=![]() .
.
结合下面图象可知,a的取值范围是![]() 或a=
或a=![]() .
.

(3)抛物线![]() 的对称轴为
的对称轴为![]() ,抛物线开口向上,当
,抛物线开口向上,当![]() 时,
时,![]() 越来越大,则
越来越大,则![]() 的x的最大值为3,可知,当
的x的最大值为3,可知,当![]() 时,不等式有最大值且最大值为0,则
时,不等式有最大值且最大值为0,则 ![]() ,代入得
,代入得![]() ,解得
,解得![]() .
.
则实数![]() 的值为8.
的值为8.

【题目】某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如下表:
餐食种类 | 价格(单位:元) |
汉堡套餐 | 40 |
鸡翅 | 16 |
鸡块 | 15 |
冰激凌 | 14 |
蔬菜沙拉 | 9 |
促销活动:
(1)汉堡套餐5折优惠,每单仅限一套;
(2)全部商品(包括打折套餐)满20元减4元,满40元减10元,满60元减15元,满80元减20元.
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份;点点想要汉堡套餐、鸡块、冰激凌各一份,若他们把想要的都买全,最少要花____________元(含送餐费).
【题目】甲乙两人依次测量同一圆柱体工件的横截面直径(单位:![]() ),测得的数据分别如表1、表2.
),测得的数据分别如表1、表2.
表1:甲的测量数据
测量数据 | 9.8 | 9.9 | 10 | 10.1 | 10.3 |
频数 | 1 | 3 | 3 | 2 | 1 |
表2:乙的测量数据
测量数据 | 9.7 | 9.8 | 10 | 10.1 | 10.3 |
频数 | 1 | 2 | 3 | 2 | 2 |
(1)如果在这些测量数据中选择一个数据作为工件直径的估计值,应该是那个数据?请说明理由.
(2)如果甲再测量一次,求他测量出的数据恰好是估计值的概率;
(3)请直接判断甲乙两人谁的测量技术更好______(填甲或乙),你选择的统计量是_______.