��Ŀ����
����Ŀ����ͼ��1������ƽ��ֱ������ϵ�У���![]() ����
����![]() ����
����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��1����λÿ����ٶ������˶���ͬʱ��
��1����λÿ����ٶ������˶���ͬʱ��![]() �ӵ�
�ӵ�![]() ��������
��������![]() ����������2����λÿ����ٶ������˶���
����������2����λÿ����ٶ������˶���![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ������
������![]() �����
�����![]() ʱ������ͬʱֹͣ�˶������˶���ʱ��Ϊ
ʱ������ͬʱֹͣ�˶������˶���ʱ��Ϊ![]() �룮�������˶������У���
�룮�������˶������У���![]() ��
��![]() ���ص����ֵ����Ϊ
���ص����ֵ����Ϊ![]() ��
��
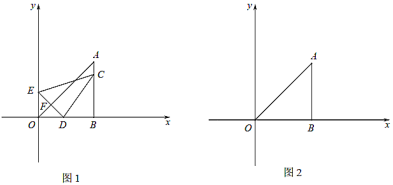
��1����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ���
���![]() ��
��![]() ��ͬһֱ���ϣ�
��ͬһֱ���ϣ�
��2����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3����ͼ��3���л���![]() ����
����![]() �ĺ���ͼ��ֱ��д��
�ĺ���ͼ��ֱ��д��![]() �����ֵ��
�����ֵ��
���𰸡���1��4����2�� ����3�����������
����3�����������![]() �����ֵ����8��
�����ֵ����8��
��������
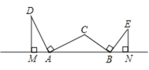
��1����ͼ1��������![]() ���
���![]() ��
��![]() ��ͬһֱ����ʱ���ɵ�
��ͬһֱ����ʱ���ɵ�![]() �ǵ���ֱ�������Σ�����
�ǵ���ֱ�������Σ�����![]() ���������t�ķ��̣��ⷽ�̼��ɣ�
���������t�ķ��̣��ⷽ�̼��ɣ�
��2���������������G����Ϊ![]() ����Ϊ
����Ϊ![]() ��������������ۣ����ø�����������ϵʽ��
��������������ۣ����ø�����������ϵʽ��
��3����������ͼ����ͼ�����ֱ��д��![]() �����ֵ����8��
�����ֵ����8��
�⣺��1���ɵ�![]() ����
����![]() �á�OABΪ����ֱ�������Σ�
�á�OABΪ����ֱ�������Σ�
��![]()
��![]()
��![]() ���ǵ���ֱ�������Σ�
���ǵ���ֱ�������Σ�
��ͼ������![]() ���
���![]() ��
��![]() ��ͬһֱ����ʱ��
��ͬһֱ����ʱ��
![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��![]() ��
��
��6-t=2t-6��
��t=4��

��2����![]() ��
�У�![]() ,
,
![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��OE=OD=2t��
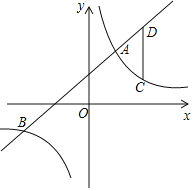
![]()
![]()
��![]()
��![]() ,
,
���G����Ϊ![]()
��ͼ2����![]() ʱ
ʱ
![]()
![]()
=![]() ��
��

��ͼ3��![]() ʱ��
ʱ��
![]()
![]()
=![]() ��
��

��ͼ4����![]() ʱ��
ʱ��
![]()
![]()

��
��3����ͼ���ɺ���ͼ���![]() �����ֵ����8��
�����ֵ����8��


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�