题目内容
【题目】对于某一函数给出如下定义:对于任意实数m, 当自变量x≥m时,函数y关于x的函数图象为![]() ,将G沿直线x=m翻折后得到的函数图象为
,将G沿直线x=m翻折后得到的函数图象为![]() ,函数G的图象由
,函数G的图象由![]() 和
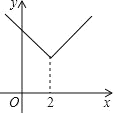
和![]() 两部分共同组成,则函数G为原函数的“对折函数”,如函数y=x(x≥2)的对折函数为
两部分共同组成,则函数G为原函数的“对折函数”,如函数y=x(x≥2)的对折函数为![]()
(1)写出函数y =2x+1(x≥ 1)的对折函数;
(2)若函数y =2x2(x≥![]() )的对折函数与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,求△ABC的周长;
)的对折函数与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,求△ABC的周长;
(3)若点P(m,5)在函数y =![]() 4( x≥1)的对折函数的图象上,求m的值;
4( x≥1)的对折函数的图象上,求m的值;
(4)当函数y=![]() 4(x≥n)的对折函数与x轴有不同的交点个数时,直接写出n的取值范围
4(x≥n)的对折函数与x轴有不同的交点个数时,直接写出n的取值范围
【答案】(1)![]() ;(2)
;(2)![]() ;(3)m=4或6;(4)①当n<1时,有4个交点;②当n=1时,有3个交点;③当1<n<3时,函数与x轴有2个交点;④当n=3时,有3个交点;⑤当n>3时,无交点
;(3)m=4或6;(4)①当n<1时,有4个交点;②当n=1时,有3个交点;③当1<n<3时,函数与x轴有2个交点;④当n=3时,有3个交点;⑤当n>3时,无交点
【解析】
(1)利用对折函数的定义求解对折后的函数与![]() 轴的交点坐标,利用待定系数法求解即可;
轴的交点坐标,利用待定系数法求解即可;
(2)先求解对折函数的解析式,得到C的坐标,利用勾股定理可得答案;
(3)先求解对折函数的解析式,把P的坐标代入即可得到答案;
(4)根据拐点的纵坐标分情况讨论,即可得到对折函数的图像,根据图像可得答案.
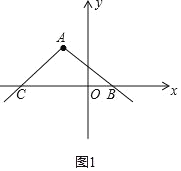
(1)如图1,设对折点为A,则点A(1,3),设对折图象与x轴的交点为A. B,
当y =2x+1=0时,x=![]() 时,即点B(
时,即点B(![]() ,0),则点C(
,0),则点C(![]() ,0),
,0),
设直线AC为:![]()
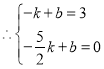
解得:![]()
所以:直线AC的表达式为:y=2x+5,
故y=2x+1(x1)的对折函数为:![]()
(2)由对折函数的定义得拐点坐标为:![]() ,
,![]() ,
,
![]()
同理可得:函数y=2x2(![]() )的对折函数
)的对折函数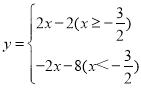
![]() 点C(0,2),
点C(0,2),
则AB=5,AC=![]() ,BC=
,BC=![]() ,
,
则△ABC的周长为:![]()
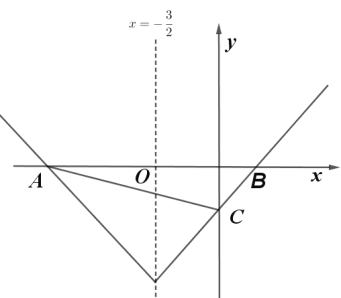
(3)令y=![]() 4=0,则x=1或3,如下图:即点A. B的坐标为(1,0)、(3,0),
4=0,则x=1或3,如下图:即点A. B的坐标为(1,0)、(3,0),
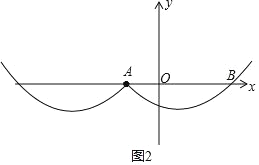
则对折后函数的顶点坐标为(3,4),该函数表达式为:y=![]() 4,
4,
即对折函数为![]()
将点P(m,5)代入y=![]() 4得:
4得:
![]()
解得:![]() (舍去)
(舍去)
将点P(m,5)代入y=![]() 4,
4,
![]()
解得:![]() (舍去)
(舍去)
综上:m=4或6
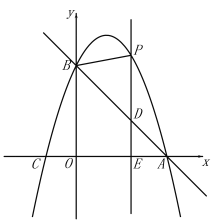
(4)①当n<1时,如图3:
此时x=n在点A(1,0)的左侧,
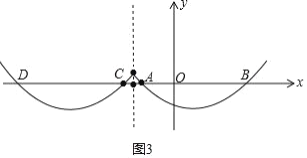
从图中可以看出:函数与x轴有4个交点(A、B. C. D);
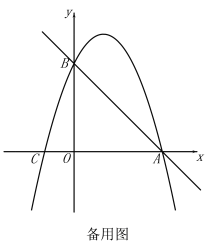
②当n=1时,x=n过点A,从图2可以看出:函数与x轴有3个交点;
③如图:同理:当1<n<3时,函数与x轴有2个交点;
④如图:同理:当n=3时,函数与x轴有3个交点;
⑤同理:当n>3时,无交点

【题目】某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如下表:
餐食种类 | 价格(单位:元) |
汉堡套餐 | 40 |
鸡翅 | 16 |
鸡块 | 15 |
冰激凌 | 14 |
蔬菜沙拉 | 9 |
促销活动:
(1)汉堡套餐5折优惠,每单仅限一套;
(2)全部商品(包括打折套餐)满20元减4元,满40元减10元,满60元减15元,满80元减20元.
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份;点点想要汉堡套餐、鸡块、冰激凌各一份,若他们把想要的都买全,最少要花____________元(含送餐费).