Question

【题目】如图1，已知抛物线顶点C（1，4），且与y轴交于点D（0，3）．

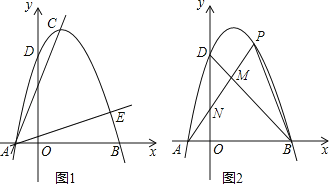
（1）求该抛物线的解析式及其与x轴的交点A、B的坐标；

（2）将直线AC绕点A顺时针旋转45°后得到直线AE，与抛物线的另一个交点为E，请求出点E的坐标；

（3）如图2，点P是该抛物线上位于第一象限的点，线段AP交BD于点M、交y轴于点N，△BMP和△DMN的面积分别为S1，S2，求S1﹣S2的最大值．

Answer 1

【答案】（1）点A、B的坐标分别为（﹣1，0）、（3，0）；（2）点E（，）；（3）S1﹣S2的最大值为．

【解析】

（1）设抛物线的表达式为：y=a（x-h）2+k=a（x-1）2+4，将点D的坐标代入上式，即可求解；
（2）构建△ACH，用解直角三角形的方法求出点H的坐标，进而求解；
（3）设S=S△ABM，则S1-S2=（S1+S）-（S+S2）=S△ABP-S△BDO，即可求解．

解：（1）设抛物线的表达式为：y＝a（x﹣h）2+k＝a（x﹣1）2+4，

将点D的坐标代入上式并解得：a＝﹣1，

故抛物线的表达式为：y＝﹣（x﹣1）2+4＝﹣x2+2x+3①；

令y＝0，则x＝﹣1或3，

故点A、B的坐标分别为：（﹣1，0）、（3，0）；

（2）如图，设函数的对称轴交x轴于点G，交AE于点H，过点H作HN⊥AC于点N，

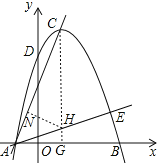
在△AGC中，tan∠ACG＝＝tan∠HCN，

在Rt△CHN中，设HN＝x，则CN＝HNtan∠HCN＝2x，

在Rt△ANH中，∠NAH＝45°，则AN＝NH＝x，

故AC＝AN+CN＝3x＝，

故x＝，

在Rt△CHN中，CH＝，

故点H（1，），

由点A、H的坐标得，直线AH的表达式为：y＝x+②，

联立①②并解得：x＝或﹣1（舍去﹣1），

故点E（，）；

（3）设点P的坐标为（x，y），y＝﹣x2+2x+3，

设S＝S△ABM，

则S1﹣S2＝（S1+S）﹣（S+S2）＝S△ABP﹣S△BDO

＝×AB×y﹣×OB×OD

＝×4×y×3×3

＝﹣2x2+4x+，

∵﹣2＜0，故S1﹣S2有最大值，

当x＝1时，其最大值为；

故S1﹣S2的最大值为．