题目内容
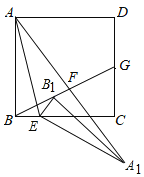
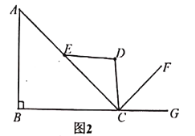
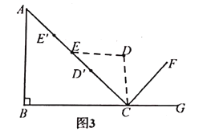
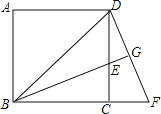
【题目】如图,正方形ABCD的边长为2,BE平分∠DBC交CD于点E,将△BCE绕点C顺时针旋转90°得到△DCF,延长BE交DF于G,则BF的长为_____.
【答案】2![]()
【解析】
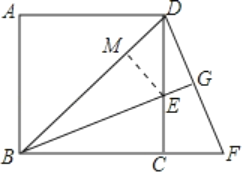
过点E作EM⊥BD于点M,则△DEM为等腰直角三角形,根据角平分线以及等腰直角三角形的性质即可得出ME的长度,再根据正方形以及旋转的性质即可得出线段BF的长.
过点E作EM⊥BD于点M,如图所示.
∵四边形ABCD为正方形,
∴∠BDC=45°,∠BCD=90°,
∴△DEM为等腰直角三角形.
∴EM=![]() DE,
DE,
∵BE平分∠DBC,EM⊥BD,
∴EM=EC,
设EM=EC=x,
∵CD=2,
∴DE=2﹣x,
∴x=![]() (2﹣x),
(2﹣x),
解得x=2![]() ﹣2,
﹣2,
∴EM=2![]() ﹣2,
﹣2,
由旋转的性质可知:CF=CE=2![]() ﹣2,
﹣2,
∴BF=BC+CF=2+2![]() ﹣2=2
﹣2=2![]() .
.
故答案为:2![]() .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某快餐店外卖促销,佳佳和点点想点外卖,每单需支付送餐费5元,每种餐食外卖价格如下表:
餐食种类 | 价格(单位:元) |
汉堡套餐 | 40 |
鸡翅 | 16 |
鸡块 | 15 |
冰激凌 | 14 |
蔬菜沙拉 | 9 |
促销活动:
(1)汉堡套餐5折优惠,每单仅限一套;
(2)全部商品(包括打折套餐)满20元减4元,满40元减10元,满60元减15元,满80元减20元.
佳佳想要汉堡套餐、鸡翅、冰激凌、蔬菜沙拉各一份;点点想要汉堡套餐、鸡块、冰激凌各一份,若他们把想要的都买全,最少要花____________元(含送餐费).