题目内容
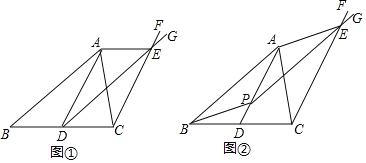
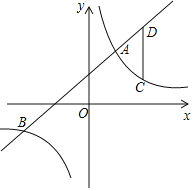
【题目】如图1,边长为6的正方形ABCD,动点P、Q各从点A,D同时出发,分别沿边AD,DC方向运动,且速度均为每秒1个单位长度.
(1)AQ与BP关系为________________;
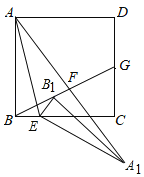
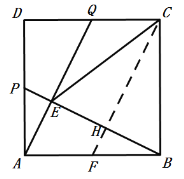
(2)如图2,当点P运动到线段AD的中点处时,AQ与BP交于点E,试探究∠CEQ和∠BCE满足怎样的数量关系;
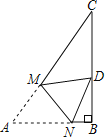
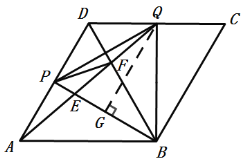
(3)如图3,将正方形变为菱形且∠BAD=60°,其余条件不变,设运动t秒后,点P仍在线段AD上,AQ交BD于F,且△BPQ的面积为S,试求S的最小值,及当S取最小值时∠DPF的正切值.
【答案】(1)AQ=BP且AQ⊥BP;(2)∠BCE=2∠CEQ;(3)![]() ;
;![]()
【解析】
(1)先利用“SAS”证得△ADQ≌△BAP,再利用角的计算,即可证得AQ⊥BP,AQ=BP;
(2)取AB中点为F,连结CF交BE于H,证得四边形QAFC是平行四边形,再证得CH所在直线是线段BE的中垂线,则CE=BC,从而求得∠BCE=2∠CEQ;
(3)先证得△BPQ为等边三角形,得到![]() ,当P到AD中点时,BP最短,从而得到S的最小值;作AM⊥CD于M,利用“SAS”证得△DPF≌△DQF,根据∠DPF=∠DQF即可求解.
,当P到AD中点时,BP最短,从而得到S的最小值;作AM⊥CD于M,利用“SAS”证得△DPF≌△DQF,根据∠DPF=∠DQF即可求解.
(1)AQ⊥BP,AQ=BP,理由如下:
∵动点P,Q各从点A,D同时出发,分别沿AD,DC方向运动,且速度均为每秒1个单位长度,
∴DQ=AP,
∵四边形ABCD是正方形,
∴AD=BA,∠ADQ=∠BAP=90°,
在△ADQ和△BAP中,
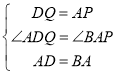 ,
,
∴△ADQ≌△BAP(SAS),
∴AQ=BP,且∠DAQ=∠ABP,
又∵∠DAQ+∠BAQ=90°,
∴∠ABP+∠BAQ=90°,
∴∠AEB=90°,
即AQ⊥BP;

(2)证明:取AB中点为F,连结CF交BE于H,
∵四边形ABCD是边长为6的正方形,
∴CD∥AB,
∵DQ=CQ=3,AF=FB=3,
∴CQ= AF,
∴四边形QAFC是平行四边形,
∴CF∥AQ,
∵AQ⊥BP,
∴CF⊥BP,
∵FH∥AE,且F为AB中点,
∴H为EB中点,即BH=EH,
∴CH所在直线是线段BE的中垂线,
∴CE=CB,
∴∠ECH=∠BCH,
∵CH∥AQ,
∴∠HCE=∠QEC,
∴∠BCE=2∠ECH=2∠CEQ,
(3)∵四边形ABCD是菱形,且∠BAD=60°,
∴AD=AB,CD∥AB,
∴△ABD为等边三角形,∠DBA=∠BDQ,
∴∠BAP=∠BDQ=60°,BD=BA,
∵动点P,Q各从点A,D同时出发,分别沿AD,DC方向运动,且速度均为每秒1个单位长度,
∴DQ=AP,
在△BDQ和△BAP中,
 ,
,
∴△BDQ≌△BAP(SAS),
∴BQ=BP,且∠DBQ=∠ABP,
又∵∠ABP +∠PBD=60°,
∴∠DBQ +∠PBD =60°,即∠PBQ=60°,
∴△BPQ为等边三角形,
作QG⊥BP于G,
∴![]() ,
,
∴![]() ,
,
当且仅当BP⊥AD时,即P到AD中点时,BP最短,
BP![]() ,
,
∴![]() ,
,
连结PF,过点A作AM⊥CD交CD延长线于M,

∵AP=PD=DQ=![]() AD=3,
AD=3,
在△DPF和△DQF中,
 ,
,
∴△DPF≌△DQF(SAS),
在Rt△ADM中,AD=6,∠ADM=180![]() -∠ADB-∠QDB =60°,
-∠ADB-∠QDB =60°,
∴![]() ,
,![]() ,
,
∴tan∠DPF=tan∠DQF=![]() .
.