题目内容
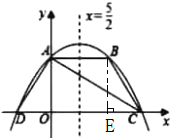
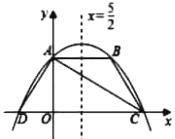
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=![]() ,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
A.点B坐标为(5,4)B.AB=ADC.a=![]() D.OCOD=16
D.OCOD=16
【答案】D
【解析】
由抛物线y=ax2+bx+4交y轴于点A,可得点A的坐标,然后由抛物线的对称性可得点B的坐标,由点B关于直线AC的对称点恰好落在线段OC上,可知∠ACO=∠ACB,再结合平行线的性质可判断∠BAC=∠ACB,从而可知AB=AD;过点B作BE⊥x轴于点E,由勾股定理可得EC的长,则点C坐标可得,然后由对称性可得点D的坐标,则OCOD的值可计算;由勾股定理可得AD的长,由交点式可得抛物线的解析式,根据以上计算或推理,对各个选项作出分析即可.
解:因为抛物线y=ax2+bx+4交y轴于点A,所以A(0,4).因为对称轴为直线x=![]() ,AB∥x轴,所以B(5,4),选项A正确,不符合题意.如答图,过点B作BE⊥x轴于点E,则BE=4,AB=5.因为AB∥x轴,所以∠BAC=∠ACO.因为点B关于直线AC的对称点恰好落在线段OC上,所以∠ACO=∠ACB,所以∠BAC=∠ACB,所以BC=AB=5.在Rt△BCE中,由勾股定理得EC=3,所以C(8,0),因为对称轴为直线x=
,AB∥x轴,所以B(5,4),选项A正确,不符合题意.如答图,过点B作BE⊥x轴于点E,则BE=4,AB=5.因为AB∥x轴,所以∠BAC=∠ACO.因为点B关于直线AC的对称点恰好落在线段OC上,所以∠ACO=∠ACB,所以∠BAC=∠ACB,所以BC=AB=5.在Rt△BCE中,由勾股定理得EC=3,所以C(8,0),因为对称轴为直线x=![]() ,所以D(-3,0).在Rt△ADO中,OA=4,OD=3,所以AD=5,所以AB=AD,选项B正确,不符合题意.设y=ax2+bx+4=a(x+3)(x-8),将A(0,4)代入得4=a(0+3)(0-8),解得a=
,所以D(-3,0).在Rt△ADO中,OA=4,OD=3,所以AD=5,所以AB=AD,选项B正确,不符合题意.设y=ax2+bx+4=a(x+3)(x-8),将A(0,4)代入得4=a(0+3)(0-8),解得a=![]() ,选项C正确,不符合题意.因为OC=8,OD=3,所以OCOD=24,选项D错误,符合题意,因此本题选D.
,选项C正确,不符合题意.因为OC=8,OD=3,所以OCOD=24,选项D错误,符合题意,因此本题选D.