题目内容
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
| 40 | 55 |
| 60 | 80 |
(1)若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?
(2)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
【答案】(1)购进![]() 种台灯85盏,购进
种台灯85盏,购进![]() 种台灯35盏;(2)购进
种台灯35盏;(2)购进![]() 种台灯30盏,购进
种台灯30盏,购进![]() 种台灯90盏时,销售总利润最大,最大值为2250元.
种台灯90盏时,销售总利润最大,最大值为2250元.
【解析】
(1)设商场应购进A型台灯x盏,B种台灯购进(120-x)盏,然后根据进货款=A型台灯的进货款+B型台灯的进货款及A,B两种台灯共120盏列出方程组求解即可;
(2)设商场销售完这批台灯可获利w元,根据获利等于两种台灯的获利总和列式整理,再求出x的取值范围,然后根据一次函数的增减性求出获利的最大值.
(1)设购进![]() 种台灯
种台灯![]() 盏,则购进
盏,则购进![]() 种台灯
种台灯![]() 盏
盏
则![]()
解得![]()
∴![]()
答:购进![]() 种台灯85盏,购进
种台灯85盏,购进![]() 种台灯35盏
种台灯35盏
(2)设购进![]() 种台灯
种台灯![]() 盏,则购进
盏,则购进![]() 种台灯
种台灯![]() 盏,设销售总利润
盏,设销售总利润![]() 元
元
则得:![]()
解得![]()
∴![]()
∵![]()
∴![]() 随着
随着![]() 的增大而减小
的增大而减小
∴当![]() 时,
时,![]() 有最大值,
有最大值,
![]()
此时![]()
答:购进![]() 种台灯30盏,购进
种台灯30盏,购进![]() 种台灯90盏时,销售总利润最大,最大值为2250元.
种台灯90盏时,销售总利润最大,最大值为2250元.

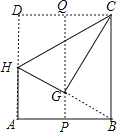
【题目】如图,在![]() 中,
中,![]() ,P是
,P是![]() 上的动点,D是
上的动点,D是![]() 延长线上的定点,连接
延长线上的定点,连接![]() 交
交![]() 于点Q.
于点Q.
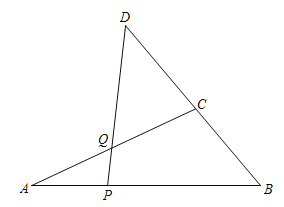
小明根据学习函数的经验,对线段![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在![]() 上的不同位置,画图测量,得到了线段
上的不同位置,画图测量,得到了线段![]() 的长度(单位:cm)的几组值,如下表:
的长度(单位:cm)的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
| 4.99 | 4.56 | 4.33 | 4.23 | 4.53 | 4.95 | 5.51 |
| 4.99 | 3.95 | 3.31 | 2.95 | 2.80 | 2.79 | 2.86 |
在![]() 的长度这三个量中,确定_________的长度是自变量,_________的长度和_________的长度都是这个自变量的函数;
的长度这三个量中,确定_________的长度是自变量,_________的长度和_________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
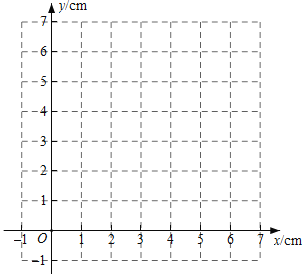
(3)结合函数图象,解决问题:当![]() 时,
时,![]() 的长度约为_______cm.
的长度约为_______cm.
【题目】某租赁公司有![]() 型两种客车,它们的载客量和租金标准如下:
型两种客车,它们的载客量和租金标准如下:
客车类型 | 载客量(人/辆) | 租金(元/辆) |
| 45 | 400 |
| 30 | 280 |
如果某学校计划组织195名师生到培训基地参加社会实践活动,那么租车的总费用最低为____________________元.