Question

【题目】已知四边形是菱形，的两边分别与射线相交于点，且

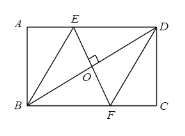
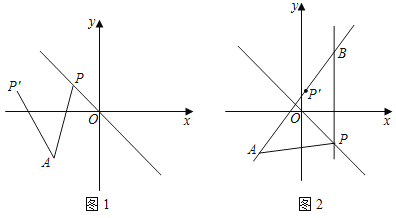
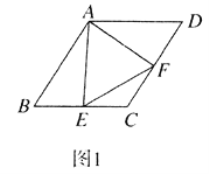
如图1，当点是线段的中点时，求证：；

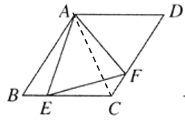
如图2，当点是线段上任意一点时(点不与重合)，求证：；

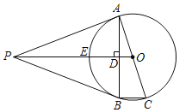
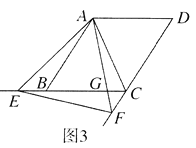
如图3，当点在线段的延长线上时，设交于点求证：．

Answer 1

【答案】（1）详见解析；（2）详见解析；（2）详见解析

【解析】

（1）通过菱形可知AB=AD，∠B=∠D，然后通过是线段的中点，可知BE=DF，即可得到，从而可得到答案；

（2）连，通过条件去证即可得到；

（3）通过两组对应角相等得到，然后得到，再由可得到AE=AF，从而得到答案．

∵四边形是菱形，

∴AB=AD=BC=CD，∠B=∠D，

∵是线段的中点，

∴BE=DF，

在和中

∴，

又

为等边三角形

连，

∵四边形是菱形，

∴AB=AD=BC=CD，∠B=∠D，

∵，

∴△ABC是等边三角形，同理△ADC是等边三角形，

∴∠BAC=∠ACD=60°，AB=AC，

∴∠BAE+∠EAC=60°，∠FAC+∠EAC=60°，

∴∠FAC=∠BAE，

在和中

∴

∴

∵四边形是菱形，

∴AB∥CD，

∴，

又∵

∴

同（2）中方法可得，

即