题目内容
【题目】如图,在一张矩形纸片 ABCD中,AB=3,点P,Q分别是AB和CD的中点,现将这张纸片折叠,使点D落到PQ上的点G处,折痕为CH,若HG的延长线恰好经过点B,则AD的长为_____.
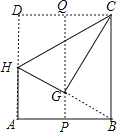
【答案】![]()
【解析】
先判断出BG=HG,进而判断出∠BCG=∠HCG,即得出∠DCH=∠GCH=∠BCG=![]() ∠BCD=30°,即:△BCH是等边三角形,即可得出AD=BC=BH,在最后用勾股定理求出BH即可得出结论.
∠BCD=30°,即:△BCH是等边三角形,即可得出AD=BC=BH,在最后用勾股定理求出BH即可得出结论.
∵P,Q是矩形ABCD的边AB,CD的中点,
∴AD=BC,∠ABC=∠BCD=∠D=90°,PQ//AD,
∵点B,G,H在同一条直线上,且点P是AB的中点,
∴BG=HG(经过三角形一边的中点平行于一边的直线必平分另一边),
由折叠知,∠CGH=∠CGB=∠D=90°,
∴CH=CB,
∵∠CGH=90°,
∴∠BCG=∠HCG,
由折叠知,∠DCH=∠HCG,即:∠DCH=∠GCH=∠BCG=![]() ∠BCD=30°,
∠BCD=30°,
∴∠BCH=60°,
∵CH=CB,
∴△BCH是等边三角形,
∴∠CBH=60°,BC=BH,即:AD=BC=BH,
在Rt△ABH中,∠ABH=∠ABC﹣∠CBH=30°,AB=3,
设AH=x,则BH=2x,
根据勾股定理得,BH2﹣AH2=AB2,
即:4x2﹣x2=9,
∴x=![]() ,
,
∴BH=2x=2![]() ,
,
即:AD=BC=BH=2![]() ,
,
故答案为2![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
| 40 | 55 |
| 60 | 80 |
(1)若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?
(2)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
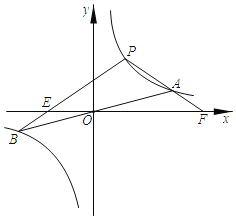
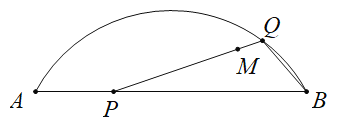
【题目】如图,M是弦![]() 与弧
与弧![]() 所围成的图形的内部的一个定点,P是弦
所围成的图形的内部的一个定点,P是弦![]() 上一动点,连接
上一动点,连接![]() 并延长交弧
并延长交弧![]() 于点Q,连接
于点Q,连接![]() .
.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,P,Q两点间距离为
,P,Q两点间距离为![]() ,
,![]() 两点间距离为
两点间距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了![]() 与x的几组对应值,补全下表:
与x的几组对应值,补全下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5.24 | 4.24 | 3.24 | 1.54 | 1.79 | 3.47 | |
| 1.31 | 1.34 | 1.42 | 1.54 | 1.80 | 2.45 | 3.47 |
(2)在同一平面直角坐标系![]() 中,描出表中各组数值对应的点
中,描出表中各组数值对应的点![]() 和
和![]() 并画出函数
并画出函数![]() 的图象;
的图象;
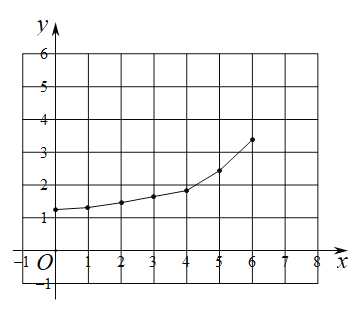
(3)结合函数图象,解决问题:当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约_________
的长度约_________![]() .(精确到0.1)
.(精确到0.1)