题目内容
【题目】如图,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 上的两个动点(不与点
上的两个动点(不与点![]() 重合),且
重合),且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() .
.
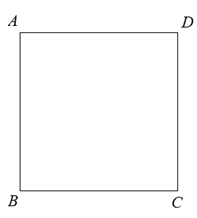
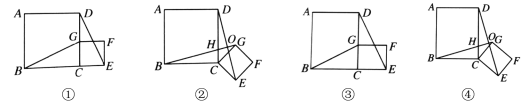
(1)依题意将图形补全;
(2)小华通过观察、实验、提出猜想:在点![]() 运动过程中,始终有
运动过程中,始终有![]() .经过与同学们充分讨论,形成了几种证明的想法:
.经过与同学们充分讨论,形成了几种证明的想法:
想法一:连接![]() ,证明
,证明![]() 是等腰直角三角形;
是等腰直角三角形;
想法二:过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于
的延长线于![]() ,可得
,可得![]() 是等腰直角三角形,证明
是等腰直角三角形,证明![]() ;
;
……
请参考以上想法,帮助小华证明![]() .(写出一种方法即可)
.(写出一种方法即可)
【答案】(1)图见解析;(2)想法一的证明见解析;想法二的证明见解析.
【解析】
(1)先分别在![]() 上取点
上取点![]() ,使得
,使得![]() ,再延长
,再延长![]() 到
到![]() ,使
,使![]() ,然后连接
,然后连接![]() 即可;
即可;
(2)想法一:先根据正方形的性质、三角形全等的判定定理与性质得出![]() ,
,![]() ,再根据角的和差、等量代换可得
,再根据角的和差、等量代换可得![]() ,从而可得
,从而可得![]() 是等腰直角三角形,然后根据等腰直角三角形的性质可得
是等腰直角三角形,然后根据等腰直角三角形的性质可得![]() ,最后根据垂线平分线的判定与性质可得
,最后根据垂线平分线的判定与性质可得![]() ,由此即可得证;
,由此即可得证;
想法二:先根据正方形的性质、三角形全等的判定定理与性质得出![]() ,从而可得
,从而可得![]() 是等腰直角三角形,再根据等腰直角三角形的性质可得
是等腰直角三角形,再根据等腰直角三角形的性质可得![]() ,然后根据三角形全等的判定定理与性质得出
,然后根据三角形全等的判定定理与性质得出![]() ,由此即可得证.
,由此即可得证.
(1)先分别在![]() 上取点
上取点![]() ,使得
,使得![]() ,再延长
,再延长![]() 到
到![]() ,使
,使![]() ,然后连接
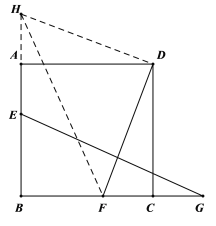
,然后连接![]() ,补全图形如下所示:
,补全图形如下所示:
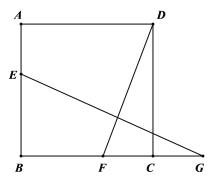
(2)想法一:如图,连接![]()
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,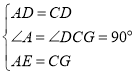
![]()
![]() ,
,![]()
![]()
![]() ,即
,即![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]()
又![]()
![]() 是线段FG的垂直平分线
是线段FG的垂直平分线
![]()
![]() ;
;

想法二:如图,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于
的延长线于![]() ,连接HF
,连接HF
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,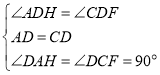
![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]()
![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,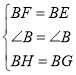
![]()
![]()
![]() .
.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】五名学生投篮球,每人投10次,统计他们每人投中的次数.得到五个数据,并对数据进行整理和分析给出如下信息:
平均数 | 中位数 | 众数 |
m | 6 | 7 |
则下列选项正确的是( )
A.可能会有学生投中了8次
B.五个数据之和的最大值可能为30
C.五个数据之和的最小值可能为20
D.平均数m一定满足![]()
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
| 40 | 55 |
| 60 | 80 |
(1)若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?
(2)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).