题目内容
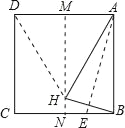
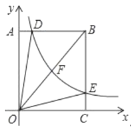
【题目】如图，反比例函数
的图象分别与矩形
的边
，
相交于点
，
，与对角线
交于点
，以下结论：
①若
与
的面积和为2，则
；
②若
点坐标为
，
，则
；
③图中一定有
；
④若点是的中点，且
，则四边形
的面积为18．
其中一定正确个数是（ ）
A.1B.2C.3D.4
【答案】C
【解析】
①根据反比例函数比例系数
的几何意义，可知
与
的面积相等，均为1，据此即可求出的值；
②根据
点坐标为
，
，求出
、
的长，计算出
的面积，据此即可求出的值；
③根据与的面积相等，列出等式
，然后写成比例式
，再转化为
，然后利用合比性质解答．
④根据反比例函数的几何意义，求出
，进而得出
，再求出
，从而得到四边形
的面积．
解：①
、
均在反比例函数图象上，
，
又
与的面积和为2，
，
；故本选项正确；
②
点坐标为，
，
，
，
，，
；故本选项错误；
③与的面积相等，
，
，
，
，
，
，故本选项正确；
④过F点作
交OC于G点，过F点作
交OA于H点，
，
，
又∵点
是
的中点，
，
，
，故本选项正确；
总上所述，正确的有3个，
故选：C．
练习册系列答案
相关题目
