题目内容
【题目】如图,在![]() 中,
中,![]() ,P是
,P是![]() 上的动点,D是
上的动点,D是![]() 延长线上的定点,连接
延长线上的定点,连接![]() 交
交![]() 于点Q.
于点Q.
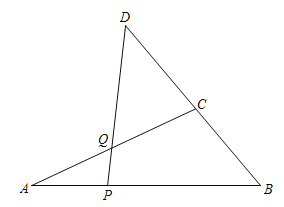
小明根据学习函数的经验,对线段![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在![]() 上的不同位置,画图测量,得到了线段
上的不同位置,画图测量,得到了线段![]() 的长度(单位:cm)的几组值,如下表:
的长度(单位:cm)的几组值,如下表:
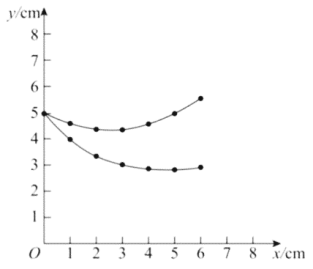
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
| 4.99 | 4.56 | 4.33 | 4.23 | 4.53 | 4.95 | 5.51 |
| 4.99 | 3.95 | 3.31 | 2.95 | 2.80 | 2.79 | 2.86 |
在![]() 的长度这三个量中,确定_________的长度是自变量,_________的长度和_________的长度都是这个自变量的函数;
的长度这三个量中,确定_________的长度是自变量,_________的长度和_________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当![]() 时,
时,![]() 的长度约为_______cm.
的长度约为_______cm.
【答案】(1)![]() ;(2)图形见解析;(3)2
;(2)图形见解析;(3)2
【解析】
(1)根据变量的定义即可求解;
(2)依据表格中的数据描点、连线即可得;
(3)画出直线AP的图象y=x,画出![]() (DP+DQ)的函数图象,两函数图象交点的横坐标即为所求.
(DP+DQ)的函数图象,两函数图象交点的横坐标即为所求.
解:(1)根据变量的定义,AP是自变量,DP、DQ是因变量,即DP、DQ是AP的函数,
(2)如图所示:
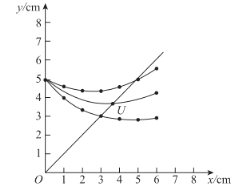
(3)在图象上画出直线AP的图象y=x,画出![]() (DP+DQ)的函数图象,新画的两个函数的交点U,即为AP=
(DP+DQ)的函数图象,新画的两个函数的交点U,即为AP=![]() (DP+DQ)的点,此时AP的长度约为3.63.
(DP+DQ)的点,此时AP的长度约为3.63.

【题目】五名学生投篮球,每人投10次,统计他们每人投中的次数.得到五个数据,并对数据进行整理和分析给出如下信息:
平均数 | 中位数 | 众数 |
m | 6 | 7 |
则下列选项正确的是( )
A.可能会有学生投中了8次
B.五个数据之和的最大值可能为30
C.五个数据之和的最小值可能为20
D.平均数m一定满足![]()
【题目】2020年是5G爆发元年,三大运营商都在政策的支持下,加快着5G建设的步伐.某通信公司实行的5G畅想套餐,部分套餐资费标准如下:
套餐类型 | 月费(元/月) | 套餐内包含内容 | 套餐外资费 | ||
国内数据流量(GB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
套餐1 | 128 | 30 | 200 | 每5元1GB,用满3GB后每3元1GB,不足部分按照0.03/元MB收取 | 0.19元/分钟 |
套餐2 | 158 | 40 | 300 | ||
套餐3 | 198 | 60 | 500 | ||
套餐4 | 238 | 80 | 600 | ||
小武每月大约使用国内数据流量49GB,国内主叫350分钟,若想使每月付费最少,则他应预定的套餐是( )
A.套餐1B.套餐2C.套餐3D.套餐4
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
| 40 | 55 |
| 60 | 80 |
(1)若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?
(2)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).