题目内容
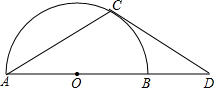
如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.
(1)求证:①点F是BD中点;②CG是⊙O的切线;
(2)若FB=FE=2,求⊙O的半径.
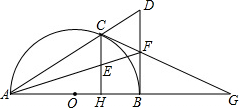
(1)求证:①点F是BD中点;②CG是⊙O的切线;
(2)若FB=FE=2,求⊙O的半径.

(1)证明:①∵CH⊥AB,DB⊥AB,
∴△AEH∽△AFB,△ACE∽△ADF;
∴
=
=
.
∵HE=EC,
∴BF=FD,即点F是BD中点.
②证明:连接CB、OC;
∵AB是直径,
∴∠ACB=90°.
∵F是BD中点,
∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO.
∴∠OCF=90°,
又∵OC为圆O半径,
∴CG是⊙O的切线.
(2)∵FC=FB=FE,
∴∠FCE=∠FEC.
∵∠FEC=∠AEH,
∴∠FCE=∠AEH,
∵∠G+∠FCE=90°,∠FAB+∠AEH=90°,
∴∠G=∠FAB,
∴FA=FG,
∵FB⊥AG,
∴AB=BG.
∵(2+FG)2=BG×AG=2BG2①
∵BG2=FG2-BF2②
由①、②得:FG2-4FG-12=0
∴FG1=6,FG2=-2(舍去)
∴AB=BG=4
.
∴⊙O半径为2
.
∴△AEH∽△AFB,△ACE∽△ADF;
∴
| EH |
| BF |
| AE |
| AF |
| CE |
| FD |
∵HE=EC,
∴BF=FD,即点F是BD中点.
②证明:连接CB、OC;
∵AB是直径,
∴∠ACB=90°.

∵F是BD中点,
∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO.
∴∠OCF=90°,
又∵OC为圆O半径,
∴CG是⊙O的切线.
(2)∵FC=FB=FE,
∴∠FCE=∠FEC.
∵∠FEC=∠AEH,
∴∠FCE=∠AEH,
∵∠G+∠FCE=90°,∠FAB+∠AEH=90°,
∴∠G=∠FAB,
∴FA=FG,
∵FB⊥AG,
∴AB=BG.
∵(2+FG)2=BG×AG=2BG2①
∵BG2=FG2-BF2②
由①、②得:FG2-4FG-12=0
∴FG1=6,FG2=-2(舍去)
∴AB=BG=4
| 2 |
∴⊙O半径为2
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 限,点C的坐标为(0,-2),过B点作BE⊥CD于点E.
限,点C的坐标为(0,-2),过B点作BE⊥CD于点E. =4cm,AB=5cm,⊙O的半径R=4.5cm,此时P点到圆心O的距离是______cm.
=4cm,AB=5cm,⊙O的半径R=4.5cm,此时P点到圆心O的距离是______cm.