题目内容
如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠D=30°．
（l）求证：CD是⊙O的切线；
（2）若CD=3
，求扇形0AC的面积．（结果保留π）
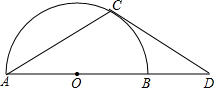
（l）求证：CD是⊙O的切线；
（2）若CD=3
| 3 |
（1）证明：连接OC，
∵AC=CD，且∠D=30°，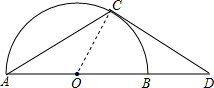
∴∠A=∠D=30°，
又∵OA=OC，
∴∠ACO=∠A=30°，
∴∠COD=∠ACO+∠A=60°，
∴∠OCD=180°-60°-30°=90°，
∴DC是⊙O的切线；
（2）由（1）得△OCD是直角三角形，
∵在Rt△OCD中，CD=3
，∠D=30°，
∴OC=CDtan30°=3
×
=3，
∴S扇形OAC=
=π．
∵AC=CD，且∠D=30°，
∴∠A=∠D=30°，
又∵OA=OC，
∴∠ACO=∠A=30°，
∴∠COD=∠ACO+∠A=60°，
∴∠OCD=180°-60°-30°=90°，
∴DC是⊙O的切线；
（2）由（1）得△OCD是直角三角形，
∵在Rt△OCD中，CD=3
| 3 |
∴OC=CDtan30°=3
| 3 |
| ||
| 3 |
∴S扇形OAC=
| 120π×3 |
| 360 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
交点）．设与AB、l、x轴相切的⊙O1的半径为r1，与AC、l、x轴相切的⊙O2半径为r2
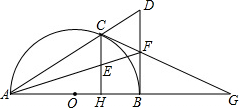
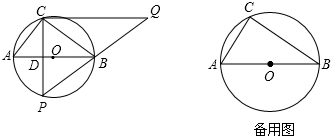点P，tan∠CAB=
AD1D与△ED1F是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由．