题目内容
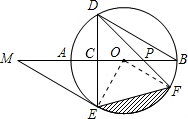
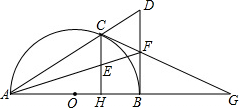
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,连接BD,过点E作EM ∥BD,交BA的延长线于点M.
∥BD,交BA的延长线于点M.
(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠APD=45°时,求图中阴影部分的面积.
 ∥BD,交BA的延长线于点M.
∥BD,交BA的延长线于点M.(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠APD=45°时,求图中阴影部分的面积.
(1)连接OE.
∵DE垂直平分半径OA,
∴OC=
OA
∵OA=OE,
∴OC=
OE,CE=
DE=
,
∴∠OEC=30°,
∴OE=
=
=
;
(2)证明:由(1)知:∠AOE=60°,
=
,
∴∠B=
∠AOE=30°,
∴∠BDE=60°
∵BD∥ME,
∴∠MED=∠BDE=60°,
∴∠MEO=∠MED+∠OEC=60°+30°=90°,
∴OE⊥EM,
∴EM是⊙O的切线;
(3)连接OF.
∵∠DPA=45°,
∵∠DCB=90°,
∴∠CDP=45°,
∴∠EOF=2∠EDF=90°,
∴S阴影=S扇形EOF-S△EOF=
-
×
×
=
π-
.
∵DE垂直平分半径OA,
∴OC=
| 1 |
| 2 |
∵OA=OE,
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴∠OEC=30°,
∴OE=
| EC |
| cos30° |
| ||||
|
| 3 |
(2)证明:由(1)知:∠AOE=60°,
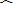 |
| AE |
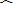 |
| AD |
∴∠B=
| 1 |
| 2 |
∴∠BDE=60°
∵BD∥ME,
∴∠MED=∠BDE=60°,
∴∠MEO=∠MED+∠OEC=60°+30°=90°,
∴OE⊥EM,
∴EM是⊙O的切线;
(3)连接OF.
∵∠DPA=45°,
∵∠DCB=90°,
∴∠CDP=45°,
∴∠EOF=2∠EDF=90°,
∴S阴影=S扇形EOF-S△EOF=
90π×(
| ||
| 360 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 4 |
| 3 |
| 2 |


练习册系列答案
相关题目
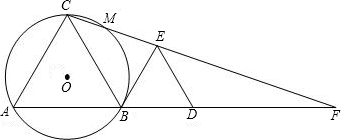
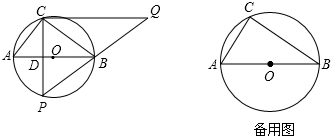 点P,tan∠CAB=
点P,tan∠CAB=


 AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.
AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.