题目内容
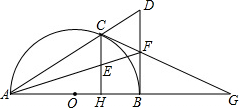
如图,以AB为直径的半圆O交AC于点D,且点D为AC的中点,DE⊥BC于点E,AE交半圆O于点F,BF的延长线交DE于点G.
(1)求证:DE为半圆O的切线;
(2)若GE=1,BF=
,求EF的长.
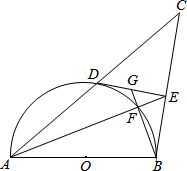
(1)求证:DE为半圆O的切线;
(2)若GE=1,BF=
| 3 |
| 2 |

(1)证明:连接OD,如图,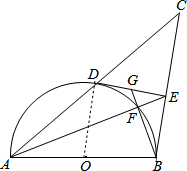
∵AB为半圆O的直径,D为AC的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥DO,
又∵点D在圆上,
∴DE为半圆O的切线;
(2)∵AB为半圆O的直径,
∴∠AFB=90°,
而DE⊥BC,
∴∠GEB=∠GFE=90°,
∵∠BGE=∠EGF,
∴△BGE∽△EGF
∴
=
,
∴GE2=GF•GB=GF(GF+BF)
∵GE=1,BF=
,
∴GF=
,
在Rt△EGF中,EF=
=
.

∵AB为半圆O的直径,D为AC的中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥DO,
又∵点D在圆上,
∴DE为半圆O的切线;
(2)∵AB为半圆O的直径,
∴∠AFB=90°,
而DE⊥BC,
∴∠GEB=∠GFE=90°,
∵∠BGE=∠EGF,
∴△BGE∽△EGF
∴
| GE |
| GB |
| GF |
| GE |
∴GE2=GF•GB=GF(GF+BF)
∵GE=1,BF=
| 3 |
| 2 |
∴GF=
| 1 |
| 2 |
在Rt△EGF中,EF=
| GE2-GF2 |
| ||
| 2 |

练习册系列答案
相关题目

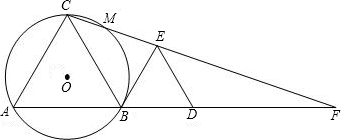


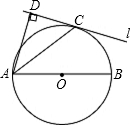


 AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.
AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.