题目内容

如图，已知Rt△ABC的斜边AB=8cm，AC=4cm．
（1）以点C为圆心作圆，当半径为多长时，直线AB与⊙C相切？为什么？
（2）以点C为圆心，分别以2cm和4cm为半径作两个圆，这两个圆与直线AB分别有怎样的位置关系？
（1）过C作CD⊥AB，交AB于点D，如图所示：

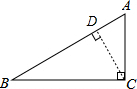
Rt△ABC的斜边AB=8cm，AC=4cm，
根据勾股定理得：BC=4
3
cm，
∵S△ABC=
1
2
AB•CD=
1
2
AC•BC，
∴CD=
AC•BC
AB
=2
3
cm，
则以点C为圆心，当半径为2
3
cm时，AB与⊙C相切；
（2）∵2＜2
3
＜4
∴以点C为圆心，分别以2cm和4cm为半径作两个圆，这两个圆与直线AB分别相离和相交；
练习册系列答案
相关题目
如图，已知△ABC是等腰三角形，∠C=90°，AC=BC=
2
，在BC上取一点O，以O为圆心，OC为半径作半圆与AB相切于点E，则⊙O的半径为______．
Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，2.5cm为半径的圆与AB的位置关系是（　　）
A．相离B．相交C．相切D．无法确定
如图，点A、B、C分别是⊙O上的点，∠B=60°，AC=3，CD是⊙O的直径，P是CD延长线上的一点，且AP=AC．
（1）求证：AP是⊙O的切线；
（2）求PD的长．
如图，已知等边△ABC，以BC为直径作半⊙O交AB于D，DE⊥AC于点E．
（1）求证：DE是半⊙O的切线；
（2）若DE=
3
，求△ABC与半⊙O重合部分的面积．
如图∠BAC=60°，半径长1的⊙O与∠BAC的两边相切，P为⊙O上一动点，以P为圆心，PA长为半径的⊙P交射线AB、AC于D、E两点，连接DE，则线段DE长度的最大值为（　　）
A．3B．6C．
3
3
2
D．3
3
如图，CA，CB分别与⊙O相切于点D，B，圆心O在AB上，AB与⊙O的另一交点为E，AE=2，⊙O的半径为1，则BC的长为（　　）
A．
2
B．2
2
C．
2
2
D．
3
如图，B为线段AD上一点，△ABC和△BDE都是等边三角形，连接CE并延长交AD的延长线于点F，△ABC的外接圆⊙O交CF于点M．
（1）求证：BE是⊙O的切线；
（2）求证：AC2=CM•CF；
（3）若CM=
2
7
7
，MF=
12
7
7
，求BD；
（4）若过点D作DG∥BE交EF于点G，过G作GH∥DE交DF于点H，则易知△DGH是等边三角形．设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3，试探究S1、S2、S3之间的等量关系，请直接写出其结论．
如图，已知：C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交直线AB于点G．
（1）求证：①点F是BD中点；②CG是⊙O的切线；
（2）若FB=FE=2，求⊙O的半径．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网