题目内容
在△ABC中,P是BC边上的一个动点,以AP为直径的⊙O分别交AB、AC于点E和点F.
(1)若∠BAC=45°,EF=4,则AP的长为多少?
(2)在(1)条件下,求阴影部分面积.
(3)试探究:当点P在何处时,EF最短?请直接写出你所发现的结论,不必证明.
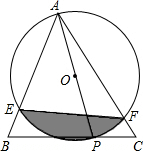
(1)若∠BAC=45°,EF=4,则AP的长为多少?
(2)在(1)条件下,求阴影部分面积.
(3)试探究:当点P在何处时,EF最短?请直接写出你所发现的结论,不必证明.

(1)连接OE、OF.
∵∠EOF=2∠EAF,∠EAF=45°,
∴∠EOF=90°;
∴△EOF是等腰直角三角形,
∴OE=
EF=2
,
∴直径AP=2OE=4
;
(2)S阴影=S扇形EOF-S△EOF=
-
×2
×2
=2π-4;
(3)在三角形OEP中,根据垂径定理和勾股定理知,当OP取最小值时,EF的值最小;又根据点到直线的距离垂线段最短垂线段最短知当AP⊥BC时,AP最短.
所以当AP⊥BC时,EF最短.
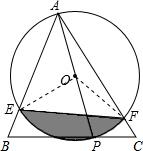
∵∠EOF=2∠EAF,∠EAF=45°,
∴∠EOF=90°;
∴△EOF是等腰直角三角形,
∴OE=
| ||
| 2 |
| 2 |
∴直径AP=2OE=4
| 2 |
(2)S阴影=S扇形EOF-S△EOF=
90π•(2
| ||
| 360 |
| 1 |
| 2 |
| 2 |
| 2 |
(3)在三角形OEP中,根据垂径定理和勾股定理知,当OP取最小值时,EF的值最小;又根据点到直线的距离垂线段最短垂线段最短知当AP⊥BC时,AP最短.
所以当AP⊥BC时,EF最短.


练习册系列答案
相关题目