题目内容
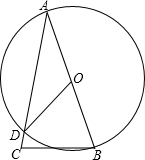
如图，CD与AB是⊙O内两条相交的弦，且AB为⊙O的直径，CE⊥AB于点E，CE=5，连接AC、BD．
（1）若sinD=
，则cosA=______；
（2）在（1）的条件下，求BE的长．
（1）若sinD=
| 5 |
| 13 |
（2）在（1）的条件下，求BE的长．
（1）∵AB是⊙O的直径，
∴∠ACB=90°（直径所对的圆周角是直角）；
∵∠A=∠D（同弧所对的圆周角相等），
∴sin∠D=sin∠D=
=
；
又∵CE=5，
∴AC=13，
∴AE=12（勾股定理），
∴cosA=
=
．…（2分）
（2）如图，连接BC．
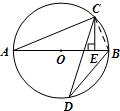∵AB为⊙O的直径，∴∠ACB=90°．
∴由（1）知AC=13，AE=12，cosA=
．
在Rt△ACB中，cosA=
，
∴AB=
．…（4分）
∴BE=AB-AE=
．…（5分）
∴∠ACB=90°（直径所对的圆周角是直角）；
∵∠A=∠D（同弧所对的圆周角相等），
∴sin∠D=sin∠D=
| CE |
| AC |
| 5 |
| 13 |
又∵CE=5，
∴AC=13，
∴AE=12（勾股定理），
∴cosA=
| AE |
| AC |
| 12 |
| 13 |
（2）如图，连接BC．
∵AB为⊙O的直径，∴∠ACB=90°．∴由（1）知AC=13，AE=12，cosA=
| 12 |
| 13 |
在Rt△ACB中，cosA=
| AC |
| AB |
∴AB=
| 169 |
| 12 |
∴BE=AB-AE=
| 25 |
| 12 |
练习册系列答案
阅读快车系列答案
相关题目
