题目内容
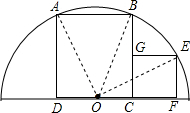
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )

A.(4+
| B.9cm | C.4
| D.6
|

连接OA、OB、OE,
∵四边形ABCD是正方形,
∴AD=BC,∠ADO=∠BCO=90°,
∵在Rt△ADO和Rt△BCO中
∵
|
∴Rt△ADO≌Rt△BCO,
∴OD=OC,
∵四边形ABCD是正方形,
∴AD=DC,
设AD=acm,则OD=OC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在△AOD中,由勾股定理得:OA=OB=OE=
| ||
| 2 |
∵小正方形EFCG的面积为16cm2,
∴EF=FC=4cm,
在△OFE中,由勾股定理得:(
| ||
| 2 |
| 1 |
| 2 |
解得:a=-4(舍去),a=8,
| ||
| 2 |
| 5 |
故选C.

练习册系列答案
相关题目