题目内容
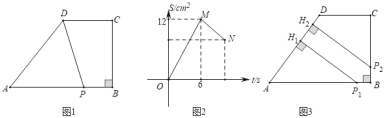
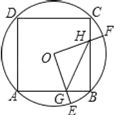
【题目】如图所示,Rt△ABC是一张放在平面直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4.将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上.
(1)在下图所示的直角坐标系中,求E点的坐标及AE的长.
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值时,A、D、M三点构成等腰三角形?并求出点M的坐标.
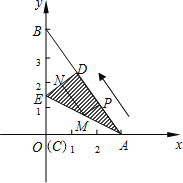
【答案】(1)E(0,![]() ),AE=
),AE=![]() ;(2)
;(2)![]() ,当t=
,当t=![]() 时,S最大=
时,S最大=![]() ;(3)当t=
;(3)当t=![]() 或
或![]() 秒时,A、D、M三点构成等腰三角形,M(
秒时,A、D、M三点构成等腰三角形,M(![]() ,
,![]() );M(3
);M(3![]() ,
,![]() ).
).
【解析】
(1)由折叠可知△AOE≌△ADE,根据全等三角形的对应边相等,以及对应角相等得到OE=ED,∠ADE=∠AOE=90°,AD=AO=3,根据勾股定理求出AB的长,设出ED=OE=x,在直角三角形BED中,根据勾股定理列出关于x的方程,求出方程的解得到x的值,进而写出点E的坐标,再在直角三角形AOE中,根据勾股定理求出AE的长即可;
(2)根据两组对边互相平行得到四边形MNDP为平行四边形,又∠ADE为直角,所以MNDP为矩形,根据题意表示出AP的长,进而得到PD的长,又由平行得到两对同位角相等,进而得到△AMP∽△AED,根据相似三角形对应边成比例得到比例式,将各自的值代入表示出PM的长,由矩形的面积公式长乘以宽和表示出的长DP与宽PM,表示出矩形的面积,得到面积与t成二次函数关系,利用二次函数求最值的方法求出面积S的最大值及取得最大值时t的值即可;
(3)根据题意发现有两种情况满足△ADM为等腰三角形,①当MD=MA时,P为AD中点,由AD求出AP,进而根据速度求出此时t的值,此时三角形AMD为等腰三角形,过M作MF垂直于x轴,根据“ASA”得到△APM≌△AFM,求出MF=MP,即为M的纵坐标,求出FA,进而求出OF的长,即为M的横坐标,写出M的坐标即可;②当AD=AM=3时,由平行的两对同位角相等,进而得到△AMP∽△AED,根据相似三角形对应边成比例得到比例式,求出AP的长,由速度求出此时t的值,此时三角形AMD为等腰三角形,过M作MF垂直于x轴,根据“ASA”得到△APM≌△AFM,同理可得M的坐标.
(1)据题意,△AOE≌△ADE,
∴OE=DE,∠ADE=∠AOE=90°,AD=AO=3,
在Rt△AOB中,AB=![]() =5,
=5,
设DE=OE=x,在Rt△BED中,根据勾股定理得:BD2+DE2=BE2,
即22+x2=(4-x)2,解得x=![]() ,∴E(0,
,∴E(0,![]() )
)
在Rt△AOE中,AE=![]() ;
;
(2)∵PM∥DE,MN∥AD,且∠ADE=90°,
∴四边形PMND是矩形,
∵AP=t×1=t,
∴PD=3-t,
∵△AMP∽△AED,
∴![]() ,
,
∴PM=![]() ,
,
∴S矩形PMND=PMPD=![]() (3t),
(3t),
∴S矩形PMND=![]() t2+
t2+![]() t或S矩形PMND=
t或S矩形PMND=![]() (t
(t![]() )2+
)2+![]() ,
,
当t=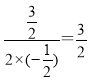 时,S最大=
时,S最大=![]() ;
;
(3)显然DM≠AD,故等腰三角形有以下二种情况:![]()
①当MD=MA时,点P是AD中点,
∴AP=![]() ,
,
∴t=![]() ÷1=
÷1=![]() (秒)
(秒)
∴当t=![]() 时,A、D、M三点构成等腰三角形,
时,A、D、M三点构成等腰三角形,
过点M作MF⊥OA于F,
∵△APM≌△AFM,
∴AF=AP=![]() ,MF=MP=
,MF=MP=![]() =
=![]() ,
,
∴OF=OA-AF=3-![]() =
=![]() ,
,
∴M(![]() ,
,![]() );
);
②当AD=AM=3时,
∵△AMP∽△AED,
∴![]() ,
,![]()
∴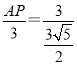 ,
,
∴AP=![]() ,
,
∴t=![]() ÷1=
÷1=![]() (秒)
(秒)
∴当t=![]() 秒时,A、D、M三点构成等腰三角形,
秒时,A、D、M三点构成等腰三角形,
过点M作MF⊥OA于F,
∵△AMF≌△AMP,
∴AF=AP=![]() ,FM=PM=
,FM=PM=![]() =
=![]() ,
,
∴OF=OA-AF=3-![]() ,
,
∴M(3![]() ,
,![]() ).
).

【题目】诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 | 成绩分组(单位:分) | 频数 |
A | 50≤x<60 | 40 |
B | 60≤x<70 | a |
C | 70≤x<80 | 90 |
D | 80≤x<90 | b |
E | 90≤x<100 | 100 |
合计 | c |
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= ;
(2)扇形统计图中,m的值为 ,“E”所对应的圆心角的度数是 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?

【题目】在“全国爱眼日”这天,某校课题小组为了了解本校![]() 名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
组别 | 视力 | 频率 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
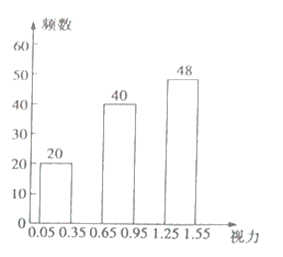
根据以上信息解答下列问题:
![]() 填空:
填空:![]() ______ _,并将频数分布直方图补充完整;
______ _,并将频数分布直方图补充完整;
![]() 若将统计结果绘制成扇形统计图,则第
若将统计结果绘制成扇形统计图,则第![]() 组所在扇形的圆心角度数为 ;
组所在扇形的圆心角度数为 ;
![]() 课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
视力 |
|
|
|
|
|
比重 |
|
|
|
|
|
根据调查结果估计该校有多少名学生的视力下降是由于过度使用电子产品.