题目内容
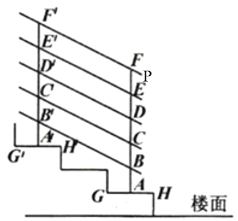
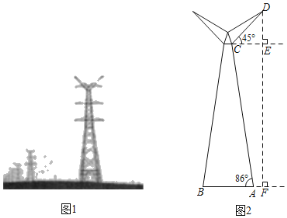
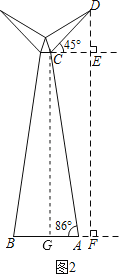
【题目】如图所示,图1,图2分别是某款高压电塔的实物图和示意图电塔的底座AB与地面平齐,DF表示电塔顶端D到地面的距离,已知AF的长是2米,支架AC与地面夹角∠BAC=86°,顶端支架DC长10米,DC与水平线CE之间夹角∠DCE=45°,求电塔的高度DF.(sin86°=0.998,cos86°=0.070,tan86°=14.300,![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
【答案】电塔的高度DF约为79米.
【解析】
过点C作CG⊥AB于G,解Rt△DCE,求出CE=DE=FG≈7,那么AG=GF﹣AF≈5.再解Rt△ACG,求出EF=CG=71.5,代入DF=DE+EF即可.
如图,过点C作CG⊥AB于G,则四边形CEFG是矩形,
∴CE=FG,CG=EF.
在Rt△DCE中,∵∠DCE=45°,CD=10,
∴DE=CDsin∠DCE=10×![]() =5
=5![]() ≈7,
≈7,
∴CE=DE=FG≈7,
∴AG=GF﹣AF≈7﹣2=5.
在Rt△ACG中,∵∠CAG=86°,AG=5,
∴CG=AGtan∠CAG=5×14.3=71.5,
∴EF=CG=71.5,
∴DF=DE+EF=7+71.5≈79(米).
答:电塔的高度DF约为79米.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目