ĖâÄŋÄÚČÝ
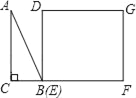
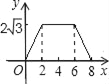
ĄūĖâÄŋĄŋČįÍžĒŲĢŽÔÚËÄąßÐÎABCDÖÐĢŽABĄÎCDĢŽĄÏB=90ĄãĢŽAB=2CDĢŪķŊĩãPīÓĩãAģö·ĒĢŽÔÚËÄąßÐÎABCDĩÄąßÉÏŅØAĄúBĄúCĩÄ·―ÏōŌÔ1cm/sĩÄËŲķČÔČËŲŌÆķŊĢŽĩ―īïĩãCĘąÍĢÖđŌÆķŊĄĢŌŅÖŠĄũAPDĩÄÃæŧýS(cm 2)ÓëĩãPÔËķŊĩÄĘąžät(s)ÖŪžäĩÄšŊĘýÍžÏóČįÍžĒÚËųĘūĢŽļųūÝĖâŌâ―âīðÏÂÁÐÎĘĖâ
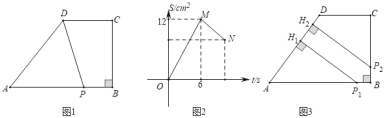
(1)ÔÚÍžĒŲÖÐĢŽAB=ĄĄ ĄĄĄĄcmĢŽ BC=ĄĄ ĄĄ ĄĄcmĢŪ
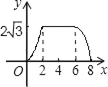
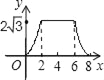
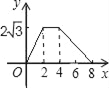
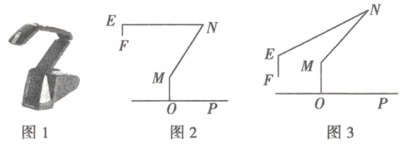
(2)ĮóÍž2ÖÐÏßķÎMNĩÄšŊĘýđØÏĩĘ―(ēĒÐīģötĩÄČĄÖĩ·ķΧ) ĢŪ
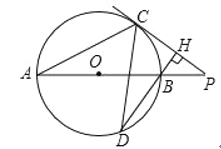
(3)ČįÍžĒÛĢŽÉčķŊĩãPÓÃÁËt1 (s)ĩ―īïĩãP1īĶĢŽÓÃÁËt2 (s)ĩ―īïĩãP2īĶĢŽ·ÖąðđýP1ĄĒP2ŨũADĩÄīđÏßĢŽīđŨãΊH1ĄĒH2ĢŪĩąP1H1= P2H2=4ĘąĢŽÁŽP1P2ĢŽĮóĄũBP1P2ĩÄÃæŧýĢŪ
Ąūīð°ļĄŋĢĻ1ĢĐ6ĢŽ4ĢŧĢĻ2ĢĐ![]() ĢĻ6ĄÜtĄÜ10ĢĐĢŧĢĻ3ĢĐ
ĢĻ6ĄÜtĄÜ10ĢĐĢŧĢĻ3ĢĐ![]()
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝĖâŌâšÍÍžÏóŋÉÖŠAB=6cmĢŽļųūÝÍžÏóŋÉÖŠĄũABDĩÄÃæŧýΊ12ĢŽļųūÝAB=2CDŋÉĩÃĄũBCDĩÄÃæŧýĢŽÔŲļųūÝĖÝÐÎĩÄÃæŧýđŦĘ―žīŋÉĩÃģöBCĩÄģĪĢŧ
ĢĻ2ĢĐļųūÝČý―ĮÐÎĩÄÃæŧýđŦĘ―ĮóģöĩãNĩÄŨøąęĢŽČŧšóĀûÓÃīýķĻÏĩĘý·ĻĢŽžīŋÉĮóģö―âÎöĘ―Ģŧ
ĢĻ3ĢĐÓÉĢĻ2ĢĐŋÉÖŠĢŽĄũAPDĩÄÃæŧýSĢĻcm2ĢĐÓëĩãPÔËķŊĩÄĘąžätĢĻsĢĐÖŪžäĩÄšŊĘýđØÏĩĘ―ĢŽČŧšóļųūÝČý―ĮÐÎĩÄÃæŧýđŦĘ――âīðžīŋÉĢŪ
―âĢšĢĻ1ĢĐļųūÝĖâŌâšÍÍžÏóŋÉÖŠAB=6cmĢŽBCĘĮÁ―Æ―ÐÐÏßĩÄūāĀëĢŽ
ĄßSĄũABDĢ―![]() ABBCĢ―
ABBCĢ―![]() ĄÁ6ĄÁBCĢ―12cm2ĢŪ
ĄÁ6ĄÁBCĢ―12cm2ĢŪ
ĄāBC=4cmĢŪ
đĘīð°ļΊĢš6Ģŧ4Ģŧ
ĢĻ2ĢĐĩąĩãPÔËķŊĩ―ĩãCĘątĢ―10ĢŽ
Ąß![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
Ąā![]() ĢŽ
ĢŽ
ĄāSĄũAPDĢ―![]() ĢŽ
ĢŽ
ĄāN(10ĢŽ6)ĢŽ
ÉčÏßķÎMNĩÄ―âÎöĘ―ÎŠĢšsĢ―at+bĢŽ
°ŅM(6ĢŽ12)N(10ĢŽ6)īúČëĩÃĢš
![]() ĢŽ―âĩÃĢš
ĢŽ―âĩÃĢš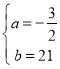 ĢŽ
ĢŽ
Ąā![]() ĢĻ6ĄÜtĄÜ10ĢĐĢŧ
ĢĻ6ĄÜtĄÜ10ĢĐĢŧ
ĢĻ3ĢĐđýĩãDŨũDEĄÍABĢŽīđŨãΊEĢŽ
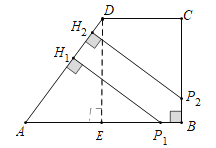
ĄßDEĢ―BCĢ―4ĢŽAEĢ―ABĐBEĢ―ABĐCDĢ―3ĢŽ
Ąā![]() ĢŽ
ĢŽ
ĄßĩąĩãPÔÚABąßÉÏĢŽžī0ĄÜtĄÜ6ĘąĢŽSĢ―2tĢŧ
ĩąĩãPÔÚBCąßÉÏĢŽžī6ĄÜtĄÜ10ĘąĢŽ![]() ĢŽ
ĢŽ
ĄßP1H1Ģ―P2H2Ģ―4ĢŽ
Ąā![]() ĢŽžī2tĢ―10ĢŽ
ĢŽžī2tĢ―10ĢŽ
―âĩÃĢšt1Ģ―5Ģŧ
Ąā![]() ĢŽžī
ĢŽžī![]() ĢŽ
ĢŽ
―âĩÃĢšt2Ģ―![]() ĢŽ
ĢŽ
Ąā![]() ĄÁ(6Ģ5) ĄÁ(
ĄÁ(6Ģ5) ĄÁ(![]() Ģ6)Ģ―
Ģ6)Ģ―![]() .
.

 ÔÄķÁŋėģĩÏĩÁÐīð°ļ
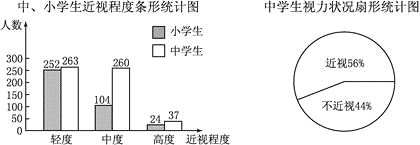
ÔÄķÁŋėģĩÏĩÁÐīð°ļĄūĖâÄŋĄŋÄģĘßēËūÏúÉĖČĨĘßēËÉúēúŧųĩØÅú·ĒÄģÖÖĘßēËĢŽŌŅÖŠÕâÖÖĘßēËĩÄÅú·ĒÁŋÔÚ20Į§ŋËÖÁ60Į§ŋËÖŪžäĢĻšŽ20Į§ŋËšÍ60Į§ŋËĢĐĘąĢŽÃŋĮ§ŋËÅú·Ē5ÔŠĢŧČôģŽđý60Į§ŋËĘĮĢŽÅú·ĒĩÄÕâÖÖĘßēËČŦēŋīō°ËÕÛĢŽĩŦÅú·ĒŨÜ―ðķîēŧĩÃÉŲÓÚ300ÔŠĢŪ
ĢĻ1ĢĐļųūÝĖâŌâĢŽĖîÐīČįąíĢš
ĘßēËĩÄÅú·ĒÁŋĢĻĮ§ŋËĢĐ | ... | 25 | 60 | 75 | 90 | ... |
ËųļķĩÄ―ðķîĢĻÔŠĢĐ | ... | 125 | 300 | ... |
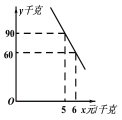
ĢĻ2ĢĐūĩũēéĢŽļÃĘßēËūÏúÉĖÏúĘÛļÃÖÖĘßēËĩÄČÕÏúĘÛÁŋ![]() ĢĻĮ§ŋËĢĐÓëÁãĘÛžÛxĢĻÔŠ/Į§ŋËĢĐĘĮŌŧīΚŊĘýđØÏĩĢŽÆäÍžÏóČįÍžĢŽĮóģö
ĢĻĮ§ŋËĢĐÓëÁãĘÛžÛxĢĻÔŠ/Į§ŋËĢĐĘĮŌŧīΚŊĘýđØÏĩĢŽÆäÍžÏóČįÍžĢŽĮóģö![]() Óë
Óë![]() ÖŪžäĩÄšŊĘýđØÏĩĘ―Ģŧ
ÖŪžäĩÄšŊĘýđØÏĩĘ―Ģŧ
ĢĻ3ĢĐČôļÃĘßēËūÏúÉĖÃŋČÕÏúĘÛīËÖÖĘßēËēŧĩÍÓÚ75Į§ŋËĢŽĮŌÁãĘÛžÛēŧąäĢŽÄĮÃīÁãĘÛžÛķĻΊķāÉŲĘąĢŽļÃūÏúÉĖÏúĘÛīËÖÖĘßēËĩÄĩąČÕĀûČóŨîīóĢŋŨîīóĀûČóĘĮķāÉŲĢŋ