Question

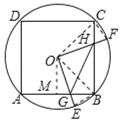
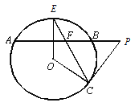
【题目】如图，边长为2的正方形ABCD内接于⊙O，点E是上一点（不与A、B重合），点F是上一点，连接OE，OF，分别与AB，BC交于点G，B，且∠EOF＝90°．有下列结论：①＝；②四边形OGBH的面积随着点E位置的变化而变化；③△GBH周长的最小值为2+；④若BG＝1﹣，则BG，GE，围成的面积是，其中正确的是_____．（把所有正确结论的序号都填上）

Answer 1

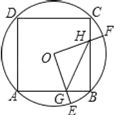
【答案】①③．

【解析】

连接OC、OB、CF、BE．①先证明，，再由，即可证明结论①正确；
②证明△BOG≌△COH，得出OG=OH，证出△OGH是等腰直角三角形，S△OBG=S△OCH，证明S四边形OGBH=S△BOC=S正方形ABCD=定值即可；
③求出AG=BH，利用等线段代换和等腰直角三角形的性质得△BGH的周长=AB+OG=2+OG，利用垂线段最短得到当OG⊥AB时，OG的长最小，此时OG=1，即可得出结论；
④求出∠BOG的度数，由扇形的面积减去三角形的面积即可得出结论．

如图所示，连接OC、OB、CF、BE．

∵∠BOE+∠BOF＝90°，∠COF+∠BOF＝90°，

∴∠BOE＝∠COF，

∴，

∵，

∴；故①正确，

在△BOG与△COH中，，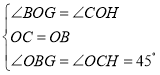

∴△BOG≌△COH（ASA），

∴OG＝OH，BG＝CH，

∵∠HOG＝90°

∴△OGH是等腰直角三角形，

∴S△OBG＝S△OCH，

∴S四边形OGBH＝S△BOC＝S正方形ABCD＝定值，故②错误；

∵AB＝BC，BG＝CH，

∴AG＝BH，

∴△BGH的周长＝BG+BH+GH＝BG+AG+OG＝AB+OG＝2+OG，

当OG⊥AB时，OG的长最小，此时OG＝1，

∴△GBH周长的最小值为2+，故③正确；

作OM⊥AB于M，则OM＝BM＝AB＝1，OB＝OM＝，

∴GM＝，

∴tan∠GOM＝＝，

∴∠GOM＝30°，

∵∠BOM＝45°，

∴∠BOG＝45°﹣30°＝15°，

∴扇形BOE的面积＝＝，

∵BG＝1﹣，

∴AG＝1+，

过G作GP⊥BO于P，

∴PG＝PB＝﹣，

∴△OBG的面积＝××（﹣）＝﹣，

∴BG，GE，围成的面积＝扇形BOE的面积﹣△BOG的面积＝﹣+，故④错误；

故答案为：①③．