Question

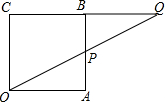
如图所示，四边形ABCD是正方形，E为BF上一点，四边形AEFC恰是一个菱形，则∠EAB=______．

Answer 1

证明：过E点作EH垂直AC交AC于H，连接BD，交AC于O点，

在正方形ABCD中，AC⊥BD，AC=BD，OB=

1

2

BD=

1

2

AC，
又∵四边形AEFC是菱形，
∴AC=CF，AC∥EF，
∵EH⊥AC，
∴∠BOH=∠OHE=∠OBE=90°，
∴四边形BEHO是矩形，
∴EH=OB，
∴EH=

1

2

AC=

1

2

AE，
在直角三角形AHE中，
sin∠EAH=

HE

AE

=

1

2

，
故∠EAH=30°，即∠EAB=∠CAB-∠EAH=45°-30°=15°．
故答案为15°．