Question

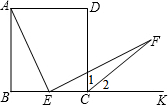
正方形ABCD，E是BC中点，∠AEF=90°，∠1=∠2
（1）线段AE与EF的数量关系为______
（2）在线段BC上，若E不是BC中点，上述关系是否成立？若成立，加以证明；若不成立，说明理由？

Answer 1

（1）取AB的中点G，
∵正方形ABCD，E是BC中点，
∴AG=BG=BE=EC，
∴△BEG是等腰直角三角形，
∴∠BGE=45°，
∠AGE=180°-45°=135°，
∵∠1=∠2，
∴∠ECF=90°+45°=135°，
∴∠AGE=∠ECF，
∵∠AEF=90°，
∴∠AEB+∠CEF=180°-90°=90°，
又∵∠BAE+∠AEB=180°-90°=90°，
∴∠BAE=∠CEF，
在△AGE和△ECF中，

∠BAE=∠CEF AG=EC ∠AGE=∠ECF

，
∴△AGE≌△ECF（ASA），
∴AE=EF；

（2）结论AE=EF仍然成立．
理由如下：在AB上截取BG=BE，
则△BGE是等腰直角三角形，
∴∠BGE=45°，
∠AGE=180°-45°=135°，
∵AG+BG=AB，BE+EC=BC，AB=BC，
∴AG=EC，
∵∠1=∠2，
∴∠ECF=90°+45°=135°，
∴∠AGE=∠ECF，
∵∠AEF=90°，
∴∠AEB+∠CEF=180°-90°=90°，
又∵∠BAE+∠AEB=180°-90°=90°，
∴∠BAE=∠CEF，
在△AGE和△ECF中，

∠BAE=∠CEF AG=EC ∠AGE=∠ECF

，
∴△AGE≌△ECF（ASA），
∴AE=EF．