题目内容
数学课上,李老师出示了这样一道题目:如图1,正方形ABCD的边长为12,P为边BC延长线上的一点,E为DP的中点,DP的垂直平分线交边DC于M,交边AB的延长线于N.当CP=6时,EM与EN的比值是多少?
经过思考,小明展示了一种正确的解题思路:过E作直线平行于BC交DC,AB分别于F,G,如图2,则可得:
=
,因为DE=EP,所以DF=FC.可求出EF和EG的值,进而可求得EM与EN的比值.
(1)请按照小明的思路写出求解过程.
(2)小东又对此题作了进一步探究,得出了DP=MN的结论,你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.

经过思考,小明展示了一种正确的解题思路:过E作直线平行于BC交DC,AB分别于F,G,如图2,则可得:
| DF |
| FC |
| DE |
| EP |
(1)请按照小明的思路写出求解过程.
(2)小东又对此题作了进一步探究,得出了DP=MN的结论,你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.

(1)过E作直线GE平行于BC交DC,AB分别于点F,G,(如图2)
则
=
,
=
,GF=BC=12,
∵DE=EP,
∴DF=FC,
∴EF=
CP=
×6=3,EG=GF+EF=12+3=15,
∴
=
=
=
;
(2)证明:正确,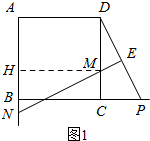
作MH∥BC交AB于点H,(如图1)
则MH=CB=CD,∠MHN=90°,
∵∠DCP=180°-90°=90°,
∴∠DCP=∠MHN,
∵NE是DP的垂直平分线,
∵∠MNH=∠CMN=∠DME=90°-∠CDP,∠DPC=90°-∠CDP,
∴∠DPC=∠MNH,
∴△DPC≌△MNH,
∴DP=MN.

则
| DF |
| FC |
| DE |
| EP |
| EM |
| EN |
| EF |
| EG |
∵DE=EP,
∴DF=FC,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| EM |
| EN |
| EF |
| EG |
| 3 |
| 15 |
| 1 |
| 5 |
(2)证明:正确,

作MH∥BC交AB于点H,(如图1)
则MH=CB=CD,∠MHN=90°,
∵∠DCP=180°-90°=90°,
∴∠DCP=∠MHN,
∵NE是DP的垂直平分线,
∵∠MNH=∠CMN=∠DME=90°-∠CDP,∠DPC=90°-∠CDP,
∴∠DPC=∠MNH,
∴△DPC≌△MNH,
∴DP=MN.


练习册系列答案
相关题目
 侧作正方形CADE和正方形CBFG,再作DD1⊥直线AB于D1,FF1⊥直线AB于F1.
侧作正方形CADE和正方形CBFG,再作DD1⊥直线AB于D1,FF1⊥直线AB于F1.





