题目内容
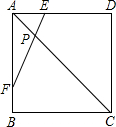
正方形ABCD中，E、F分别在边AD，AB上，且AE=BF=
AB，EF与AC交于点P．
（1）求EF：AE的值；
（2）设AB=x，四边形BCPF的面积为y，求y关于x的函数解析式．
| 1 |
| 3 |
（1）求EF：AE的值；
（2）设AB=x，四边形BCPF的面积为y，求y关于x的函数解析式．
（1）∵ABCD是正方形，
∴AB=AD，∠DAB=90°，
∵AE=BF=
AB，
∴AF=
AB，
∴EF=
AB，
∴EF：AE=
：1，
则EF：AE的值为
；
（2）过E、F点作EG⊥AC于G，FH⊥AC于H，
∵S△APF=2S△APE；S△APE+S△APF=S△AEF，
∴S△APF=
S△AEF，
∴S△AEF=AE•AF÷2=
AD×
AB÷2=
x2，
∴S正方形ABCDy=S△ABC-S△AFP=
S正方形ABCD-
S正方形ABCD=
x2．
∴AB=AD，∠DAB=90°，
∵AE=BF=
| 1 |
| 3 |
∴AF=
| 2 |
| 3 |
∴EF=
| ||
| 3 |
∴EF：AE=
| 5 |
则EF：AE的值为
| 5 |
（2）过E、F点作EG⊥AC于G，FH⊥AC于H，
∵S△APF=2S△APE；S△APE+S△APF=S△AEF，
∴S△APF=
| 2 |
| 3 |
∴S△AEF=AE•AF÷2=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 9 |
∴S正方形ABCDy=S△ABC-S△AFP=
| 1 |
| 2 |
| 2 |
| 27 |
| 23 |
| 54 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
侧作正方形CADE和正方形CBFG，再作DD1⊥直线AB于D1，FF1⊥直线AB于F1．
