题目内容
△ABC是一张等腰直角三角形纸板,∠C=90°,AC=BC=2,
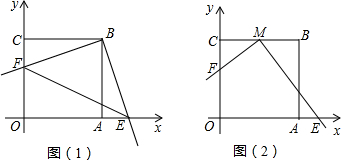
(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为s1;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2),则s2=______;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为s3,继续操作下去…,则第10次剪取时,s10=______;
(3)求第10次剪取后,余下的所有小三角形的面积之和.

(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为s1;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2),则s2=______;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为s3,继续操作下去…,则第10次剪取时,s10=______;
(3)求第10次剪取后,余下的所有小三角形的面积之和.

(1)解法1:如图甲,由题意,得AE=DE=EC,即EC=1,S正方形CFDE=12=1
如图乙,设MN=x,则由题意,得AM=MQ=PN=NB=MN=x,
∴3x=2
,
解得x=
∴S正方形PNMQ=(
)2=
又∵1>
∴甲种剪法所得的正方形面积更大.
说明:图甲可另解为:由题意得点D、E、F分别为AB、AC、BC的中点,S正方形OFDE=1.
解法2:如图甲,由题意得AE=DE=EC,即EC=1,
如图乙,设MN=x,则由题意得AM=MQ=QP=PN=NB=MN=x,
则3x=2
,
解得x=
,
又∵1>
,即EC>MN.
∴甲种剪法所得的正方形面积更大.
(2)S2=
,S10=
.
(3)解法1:探索规律可知:Sn=
剩余三角形面积和为2-(S1+S2+…+S10)=2-(1+
+…+
)=
解法2:由题意可知,
第一次剪取后剩余三角形面积和为2-S1=1=S1
第二次剪取后剩余三角形面积和为S1-S2=1-
=
=S2,
第三次剪取后剩余三角形面积和为S2-S3=
-
=
=S3,
…
第十次剪取后剩余三角形面积和为S9-S10=S10=
.
如图乙,设MN=x,则由题意,得AM=MQ=PN=NB=MN=x,
∴3x=2
| 2 |
解得x=
2
| ||
| 3 |
∴S正方形PNMQ=(
2
| ||
| 3 |
| 8 |
| 9 |
又∵1>
| 8 |
| 9 |
∴甲种剪法所得的正方形面积更大.
说明:图甲可另解为:由题意得点D、E、F分别为AB、AC、BC的中点,S正方形OFDE=1.
解法2:如图甲,由题意得AE=DE=EC,即EC=1,
如图乙,设MN=x,则由题意得AM=MQ=QP=PN=NB=MN=x,
则3x=2
| 2 |
解得x=
2
| ||
| 3 |
又∵1>
2
| ||
| 3 |
∴甲种剪法所得的正方形面积更大.
(2)S2=
| 1 |
| 2 |
| 1 |
| 29 |
(3)解法1:探索规律可知:Sn=
| 1 |
| 2n-1 |
剩余三角形面积和为2-(S1+S2+…+S10)=2-(1+
| 1 |
| 2 |
| 1 |
| 29 |
| 1 |
| 29 |
解法2:由题意可知,
第一次剪取后剩余三角形面积和为2-S1=1=S1
第二次剪取后剩余三角形面积和为S1-S2=1-
| 1 |
| 2 |
| 1 |
| 2 |
第三次剪取后剩余三角形面积和为S2-S3=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
…
第十次剪取后剩余三角形面积和为S9-S10=S10=
| 1 |
| 29 |

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目

 侧作正方形CADE和正方形CBFG,再作DD1⊥直线AB于D1,FF1⊥直线AB于F1.
侧作正方形CADE和正方形CBFG,再作DD1⊥直线AB于D1,FF1⊥直线AB于F1.