题目内容
【题目】某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为284万元?
【答案】(1)24;(2)每间商铺的年租金定为13.5万元或12万元.
【解析】试题分析:(1)租金增加30000元,少租出6间,故可租出24间;
(2)设每间商铺的年租金增加x万元,根据:租金﹣各种费用=收益,列方程求解.
试题解析:解:(1)∵30﹣(130000﹣100000)÷5000=30﹣6=24,∴能租出24间;
解:(1)30-![]() =24(间)
=24(间)
(2)设每间商铺的年租金定为![]() 万元
万元
由题意得![]() (30-
(30-![]() )=284+30-0.5×
)=284+30-0.5×![]()
整理得2![]() -51
-51![]() +324=0
+324=0
(2x-27)(x-12)=0
解: ![]() =13.5,
=13.5, ![]() =12
=12
答:每间商铺的年租金定为13.5万元或12万元.

 阅读快车系列答案
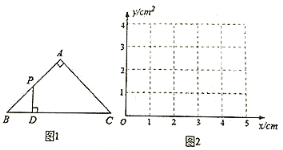
阅读快车系列答案【题目】如图1,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,点P在
,点P在![]() 的边上沿路径
的边上沿路径![]() 移动,过点P作
移动,过点P作![]() 于点D,设
于点D,设![]() ,
,![]() 的面积为
的面积为![]() (当点P与点B或点C重合时,y的值为0).
(当点P与点B或点C重合时,y的值为0).
琪琪根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是琪琪的探究过程,请补充完整:
(1)自变量x的取值范围是______________________;
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 |
| 1 |
| 2 |
| 3 |
| 4 |
y/ | 0 |
| m |
| 2 |
|
| n | 0 |
请直接写出![]() ,
,![]() ;
;
(3)在图2所示的平面直角坐标系![]() 中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图像;并结合画出的函数图像,解决问题:当
中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图像;并结合画出的函数图像,解决问题:当![]() 的面积为1
的面积为1![]() 时,请直接写出
时,请直接写出![]() 的长度(数值保留一位小数).
的长度(数值保留一位小数).
(4)根据上述探究过程,试写出![]() 的面积为y
的面积为y![]() 与
与![]() 的长度x cm之间的函数关系式,并指出自变量的取值范围.
的长度x cm之间的函数关系式,并指出自变量的取值范围.






