题目内容
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的
个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：
（1）这次调查的学生共有多少名？
（2）请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数．
（3）如果要在这个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．
【答案】（1）280名；（2）补图见解析；108°；（3）0.1.
【解析】试题分析：（1）根据“平等”的人数除以占的百分比得到调查的学生总数即可；
（2）求出“互助”与“进取”的学生数，补全条形统计图，求出“进取”占的圆心角度数即可；
（3）列表或画树状图得出所有等可能的情况数，找出恰好选到“C”与“E”的情况数，即可求出所求的概率．
试题解析：（1）56÷20%=280（名），答：这次调查的学生共有280名；
（2）280×15%=42（名），280﹣42﹣56﹣28﹣70=84（名），
补全条形统计图，如图所示，
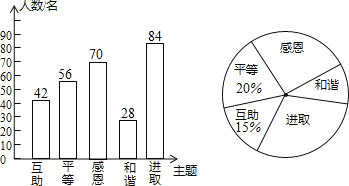
根据题意得：84÷280=30%，360°×30%=108°，
答：“进取”所对应的圆心角是108°；
（3）由（2）中调查结果知：学生关注最多的两个主题为“进取”和“感恩”用列表法为：
A | B | C | D | E | |
A | （A，B） | （A，C） | （A，D） | （A，E） | |
B | （B，A） | （B，C） | （B，D） | （B，E） | |
C | （C，A） | （C，B） | （C，D） | （C，E） | |
D | （D，A） | （D，B） | （D，E） | ||
E | （E，A） | （E，B） | （E，C） | （E，D） |
用树状图为：
共20种情况，恰好选到“C”和“E”有2种，
∴恰好选到“进取”和“感恩”两个主题的概率是0.1．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某公交车每天的支出费用为600元，每天的乘车人数x（人）与每天利润（利润＝票款收入﹣支出费用）y（元）的变化关系如下表所示（每位乘客的乘车票价固定不变）：
x（人） | … | 200 | 250 | 300 | 350 | 400 | … |
Y（元） | … | ﹣200 | ﹣100 | 0 | 100 | 200 | … |
根据表格中的数据，回答下列问题：
（1）在这个变化关系中，自变量是什么？因变量是什么？
（2）若要不亏本，该公交车每天乘客人数至少达到多少？
（3）请你判断一天乘客人数为500人时，利润是多少？
（4）试写出该公交车每天利润y（元）与每天乘车人数x（人）的关系式．
