题目内容
【题目】(感知)如图①,AC是菱形ABCD的对角线,∠B=60°,E、F分别是边BC、CD上的中点,连结AE、EF、AF.若AC=2,则CE+CF的长为_____.
(探究)如图②,在菱形ABCD中,∠B=60°.E是边BC上的点,连结AE,作∠EAF=60°,边AF交边CD于点F,连结EF.若BC=2,求CE+CF的长.
(应用)在菱形ABCD中,∠B=60°.E是边BC延长线上的点,连结AE,作∠EAF=60°,边AF交边CD延长线于点F,连结EF.若BC=2,EF⊥BC时,借助图③直接写出△AEF的周长.

【答案】【感知】2;【探究】2;【应用】![]()
【解析】
感知:根据菱形的性质即可得解;
探究:首先根据菱形的性质,进行等量转换,然后判定△ABC是等边三角形,再进行等量转换,判定△ABE≌△ACF,得出BE=CF,即可得解;
应用:首先根据菱形的性质,进行等量转换,然后判定△ABC是等边三角形,再进行等量转换,判定△ACE≌△ADF,然后判定△AEF为等边三角形,再利用勾股定理即可得出EF,进而得出△AEF的周长.
感知:∵AC是菱形ABCD的对角线,∠B=60°,
∴AB=BC=AC=CD=AD,
∵E、F分别是边BC、CD上的中点,BC=2,
∴CE+CF=BC=2;
探究:如图,连结AC.
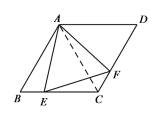
∵四边形ABCD是菱形,
∴AB=BC,AB∥CD.
∴∠B+∠BCD=180°.
∵∠B=60°,
∴△ABC是等边三角形,∠BCD=120°.
∴∠BAC=∠ACB=60°,AB=AC.
∴∠ACF=∠B=60°.
∵∠EAF=60°,
∴∠BAC﹣∠CAE=∠EAF﹣∠CAE.
∴∠BAE=∠CAF.
∴△ABE≌△ACF.
∴BE=CF.
∴CE+CF=BC=2.
应用:连接AC,如图所示:
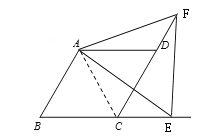
∵四边形ABCD是菱形,
∴AB=BC,AB∥CD.
∴∠B+∠BCD=180°.
∵∠B=60°,
∴△ABC是等边三角形,∠BCD=120°.
∴∠BAC=∠ACB=60°,AB=AC.
∴∠CAD=∠B=60°.
∵∠EAF=60°,
∴∠CAD﹣∠DAE=∠EAF﹣∠DAE.
∴∠CAE=∠DAF.
∵∠ACE=∠ADF,AC=AD
∴△ACE≌△ADF.
∴CE=DF,AE=AF
∵∠EAF=60°,
∴△AEF为等边三角形
∵EF⊥BC,∠ECF=60°
∴CF=2CE
∵CD=BC=2
∴CE=2
∴![]()
∴△AEF的周长为![]() .
.